CALCULO Y DISEÑO DE MAQUINAS ELECTRICAS
CAPITULO 14 - DETERMINACION DEL CAMPO MAGNETICO
Por los Ings. Jorge N. L. Sacchi - Alfredo Rifaldi
Esquemas básicos
El transformador es un objeto tridimensional, para poder calcular los esfuerzos que se presentan es necesario hacer hipótesis simplificativas que permitan una fácil esquematización.
Es muy difícil obtener una gran precisión en los cálculos, que de todos modos sería ilusorio, por lo tanto deben aceptarse métodos simplificativos.
La técnica se ha orientado considerando métodos de dos dimensiones
- Métodos planos
- Métodos cilíndricos
Los métodos planos consisten en cortar a través la columna del transformador y prolongar indefinidamente en los dos sentidos cada uno de los elementos cortados (circuito magnético, arrollamientos, cuba, tapa, etc.).
Núcleos y yugos son reemplazados por una masa magnética semiinfinita.
Las superficies externas de los lados del arrollamiento son planas.
Se desprecian escalones del núcleo, yugo, curvatura de los arrollamientos, etc.
Se presentan distintas configuraciones:
- Dentro de la ventana del circuito magnético
- Fuera de la ventana
El corte puede hacerse a lo largo del yugo, o normalmente al mismo, y en meridianos intermedios, para los cuales si el paso helicoidal de los arrollamientos es importante se nota la no alineación de los extremos.
A los transformadores de columnas son aplicables métodos planos y cilíndricos, mientras que a los acorazados sólo métodos planos.
Las paredes de la cuba durante el cortocircuito se pueden encontrar saturadas, y en esta condición todo es como si no existieran.
En cada caso deben destacarse las hipótesis simplificativas que se adoptan para que quede en claro el significado de lo que se calcula.
Métodos de cálculo
Se presentan fórmulas simples, métodos matemáticos sofisticados, métodos físicos, y gráficos.
Fórmulas simples
Sólo aplicables rigurosamente en un punto del arrollamiento, el centro.
Otras fórmulas propuestas por la bibliografía no se consideran suficientemente rigurosas.
Método plano de Roth
Consiste en resolver en coordenadas cartesianas en dos dimensiones la relación de Laplace - Poisson que liga el potencial vector magnético en cada punto con la densidad de amper vueltas en el mismo punto.
La densidad de amper vueltas se descompone en serie doble de Fourier (que puede ser simplificada).
Método cilíndrico de Roth
Este método no se utiliza en general porque conduce a cálculos demasiado voluminosos para aplicaciones prácticas.
Método cilíndrico de Rabbins
También consiste en resolver la relación de Laplace - Poisson en coordenadas polares. La densidad de corriente se representa por una serie de Fourier.
Método plano de las imágenes
Consiste en reemplazar las paredes de permeabilidad infinita, por superficies que se consideran espejos en los que se reflejan los conductores.
Se pueden presentar imágenes simples o múltiples. Se determina el campo B en cada punto y se integra la ecuación de la fórmula de Ampere (fundamental - dF = iBdl), y se resuelve el problema.
Método de los elementos finitos
Este utiliza el hecho de que la relación de Laplace - Poisson es satisfecha cuando la función de energía magnética total es mínima.
El espacio en estudio se divide en elementos triangulares (pequeños), en su interior el valor de inducción magnética se supone constante.
El método de elementos finitos puede aplicarse a problemas cilíndricos o planos.
El método de los elementos finitos permite también realizar aplicaciones tridimensionales, en las cuales la representación del transformador puede acercarse en forma sorprendente a la realidad.
Método de las diferencias finitas
Se divide el espacio con un retículo regular con distinta densidad en distintas zonas, y con límites que no necesariamente coinciden con los puntos del retículo.
El valor del campo en un punto se obtiene a partir de las ecuaciones de Poisson - Laplace expresadas en diferencias finitas.
Este método puede aplicarse tanto a problemas planos como a problemas cilíndricos.
Métodos físicos
Que utilizan cuba electrolítica, o papeles semiconductores, ambos modelos eléctricos.
La cuba electrolítica requiere la preparación de un modelo físico del problema en estudio.
Midiendo en la superficie del electrolito se determinan las líneas equipotenciales. Este método es aplicable a problemas planos y cilíndricos.
Con los papeles semiconductores se actúa en forma análoga, un dibujo con tinta conductora y luego se determinan las equipontenciales. Son naturalmente aplicables a problemas planos.
Métodos gráficos
Llamado método de Lehmann fija una serie de reglas que permiten construir en forma gráfica a partir de los contornos líneas equipotenciales y líneas de flujo, dividiendo el espacio en rectángulos (cuadrados) curvilíneos.
Un método analítico exacto es el de la representación conforme, que utiliza funciones de variable compleja transformando un campo en otro.
Comparaciones entre cálculos desarrollados
En la década de los '70 se publica en la revista Electra el informe final del grupo de trabajo del Comité de Estudio de Transformadores.
Se compararon resultados de cálculos de esfuerzos desarrollados con distintos métodos sobre transformadores definidos (monofásicos de una sola columna bobinada).
Los métodos de cálculo comparados fueron: Roth, Rabbins, imágenes, elementos finitos.
Entre los distintos métodos de cálculo se presentan diferencias en los resultados que surgen de simplificaciones que se asumen para lograr una solución práctica.
Cuando los valores de esfuerzos son pequeños las diferencias que se producen son grandes, pero estos valores no son de interés.
Para esfuerzos significativos se observa que los distintos métodos producen resultados coherentes y suficientemente precisos (errores ± 10%) dependiendo de:
- La geometría de los arrollamientos, los amper vueltas y límites del circuito magnético convenientemente definidos.
- Para los métodos que utilizan series de Fourier, el número de la armónica máxima.
- La cantidad de imágenes, al usar dicho método.
- La dimensión de las mallas de elementos en los métodos de elementos finitos.
Los comentarios que se volcaron en el trabajo citado respecto de los cuatro métodos comparados se resumen a continuación.
Para los esfuerzos axiales en el interior de la ventana, si los amper vueltas están uniformemente repartidos y equilibrados los valores calculados con los distintos métodos tienen aceptable coincidencia.
Las diferencias que pueden producirse son mayores para el arrollamiento de alta tensión.
En el exterior de la ventana las diferencias son relativamente grandes sobre todo cuando los amper vueltas no están perfectamente equilibrados.
Si se considera el máximo esfuerzo acumulado los apartamientos quedan comprendidos en el 10% del valor medio.
No se presentan diferencias significativas entre métodos planos y cilíndricos.
En casos normales la influencia del radio de curvatura es despreciable.
Cuando hay arrollamientos adyacentes, se debe considerar la totalidad de los amper vueltas dentro de la ventana.
En el caso del método cilíndrico los esfuerzos en el caso de arrollamientos adyacentes se calculan por superposición producido por cada una de las columnas consideradas separadamente.
También para los esfuerzos radiales se tiene concordancia en los resultados.
Aplicaciones - Método de las imágenes
Lógicamente la aplicación de un método cualquiera exige disponer del programa de cálculo correspondiente.
Un método de simple comprensión, que prácticamente es intuitivo es el de las imágenes.
Algunas simplificaciones pueden reducir el volumen de los cálculos.
El número de reflexiones normalmente se limita a cuatro que es suficiente a los fines prácticos.
Es posible fijar distintos números límites de reflexiones en yugos y núcleo.
El arrollamiento real para el cual se desean calcular los esfuerzos debe ser representado lo más exactamente posible.
Para el otro arrollamiento y las imágenes en cambio puede aceptarse una representación simplificada.
Las hipótesis siguientes se hacen con independencia del método de cálculo.
Para el caso de un transformador de dos arrollamientos la suma de los amper vueltas es nulo (ambos arrollamientos tienen el mismo NI), y en consecuencia la corriente magnetizante es nula.
Núcleo y yugos del circuito magnético tienen permeabilidad infinita (confirmando la hipótesis de corriente magnetizante nula).
Durante el cortocircuito las paredes metálicas de la cuba (de material magnético) están saturadas (también pueden hacerse hipótesis de paredes no saturadas, ni infinitamente permeables).
El transformador no incluye pantallas electromagnéticas, ni shunts magnéticos no saturados sobre las paredes de la cuba.
Método de las imágenes - Notas
Es un método plano en el cual el corte del arrollamiento puede ser sustituido por líneas infinitamente delgadas o puntos.
Todo el espacio se hace de permeabilidad mr = 1.
Las superficies de las masas magnéticas se representan por espejos.
Cada hilo recorrido por corriente, genera con la superficie especular un hilo imagen cuya corriente es
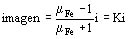
Considerando mFe > > 1 resulta K = 1 en rigor menor que 1.
Cualquiera sea la forma del conductor línea o rectángulo la reflexión se produce de igual forma.
Para los arrollamientos fuera de la ventana se presenta una reflexión, mientras que dentro de la ventana se presentan reflexiones múltiples, que en rigor son infinitas.
Con el número n de reflexiones un conductor dado se multiplica por N = 4n(n+1) + 1 si n = 1 resulta N = 9 si n = 2 en cambio N = 25.
El campo resultante se obtiene por la ley de Biot - Savart y por superposición de todos los campos individuales.
Influencia de la cuba
En las paredes laterales de las cubas y en algunos casos las tapas de los transformadores de gran potencia nominal se debe controlar el flujo de fuga para reducir pérdidas de corrientes de Foucault y evitar puntos calientes.
Se utilizan:
- Shunts magnéticos, consisten en paquetes de chapas magnéticas fijadas en el interior de la cuba, que absorben el flujo de fuga
- Pantallas electromagnéticas de material de alta conductividad (aluminio o cobre)
Cubas sin protección o con shunts dimensionados para la potencia nominal se saturan cuando se presentan las corrientes de cortocircuito, y al ocurrir esta situación es como si no existieran.
Cubas con protecciones magnéticas que no se saturan durante el cortocircuito, se pueden considerar como paredes de permeabilidad elevada (del hierro) y se debe tener en cuenta esta superficie en los cálculos.
Cubas con protección electromagnética, con placas conductoras en ellas el flujo induce corrientes de Foulcault.
Si se desprecian algunos efectos se presenta una relación lineal entre campo de fuga y campo de reacción.
El método de las imágenes en este caso considera para la pantalla.
imagen = Ki
donde K = -1, los ensayos han demostrado que se reproducen mejores las condiciones reales con K = -0.9.

Copyright 2008 - 2012 INDUCOR INGENIERIA S.A. | Todos los derechos reservados | CCS | HTML



