Advanced
Cable Testing
CALCULO Y DISEÑO DE MAQUINAS ELECTRICAS
CAPITULO 13 - ESFUERZOS DE CORTOCIRCUITO EN TRANSFORMADORES
Por los Ings. Jorge N. L. Sacchi - Alfredo Rifaldi
Introducción
Cuando ocurre un cortocircuito en una red, las corrientes de cortocircuito que circulan por los arrollamientos de un transformador los someten a esfuerzos.
Esta situación también se presenta cuando en un laboratorio de pruebas se reproducen las mismas condiciones de funcionamiento.
Los esfuerzos que se presentan se distinguen en térmicos y electrodinámicos.
Los efectos térmicos pueden evaluarse por medio de cálculo. Las normas fijan criterios para determinar la temperatura máxima que alcanza el conductor.
Los esfuerzos electrodinámicos son consecuencia de la coexistencia de las elevadas corrientes, con el campo magnético de dispersión y alcanzan valores elevados que pueden llevar el transformador al colapso, su rotura.
La importancia del problema, por sus consecuencias crece con la potencia de la máquina. Debe destacarse que la reducción de la tensión de cortocircuito es un factor que incrementa también la importancia de estos fenómenos.
Los ensayos de transformadores pueden ser ejecutados en laboratorios muy especializados cuyo número se reduce a medida que la potencia nominal del transformador crece.
La dificultad de hacer ensayos y el costo que estos tienen, ha impulsado el desarrollo de métodos de cálculo para juzgar el comportamiento de los transformadores bajo esfuerzos electrodinámicos.
Determinación de la corriente de cortocircuito
Para observar los efectos de la corriente de cortocircuito es necesario encontrar el valor representativo, se considera que este debe ser el valor máximo que puede presentarse.
Este valor surge de la tensión de alimentación, de la impedancia de la red y de las características del transformador.
La norma IEC 76-5 fija los valores de impedancia para distintos rangos de potencia de un transformador; si se trata de un transformador calculado el valor de la impedancia es conocido.
Tabla I - Valores característicos de la impedancia de cortocircuito para transformadores de dos arrollamientos
| Potencia KVA |
Impedancia % |
| Hasta 630 | 4.0 |
| 631 a 1250 | 5.0 |
| 1251 a 3150 | 6.25 |
| 3151 a 6300 | 7.15 |
| 6301 a 12500 | 8.35 |
| 12501 a 25000 | 10.0 |
| 25001 a 200000 | 12.5 |
También fija para la tensión más alta del sistema la potencia de cortocircuito en el punto de alimentación del transformador.
Tabla II - Potencia de cortocircuito aparente de un sistema
| Tensión máxima del sistema kV |
Potencia aparente de cortocircuito MVA |
| 7.2, 12, 17.5 y 24 | 500 |
| 36 | 1000 |
| 52 y 72.5 | 3000 |
| 100 y 123 | 6000 |
| 145 y 170 | 10000 |
| 245 | 20000 |
| 300 | 30000 |
| 420 | 40000 |
En base a la tensión máxima del transformador se determina la potencia de cortocircuito de la red suponiendo que se lo alimenta desde este lado.
Se debe calcular la potencia de cortocircuito (corriente) para el cortocircuito del lado contrario al devanado de alimentación
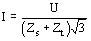kA
donde:
U: tensión máxima, o nominal según se desee lado alimentación kV
Zs = Umax12 / Pcc la impedancia de la red
Zt = Ucc ´ Un12 / (100´ POTKVA / 1000) la impedancia del transformador referida a la red (Ucc es la impedancia del transformador, Un1 la tensión nominal, POTKVA la potencia)
Estos cálculos deben ser ejecutados teniendo en cuenta las componentes resistivas y reactivas de cada impedancia.
El valor de pico de la corriente de cortocircuito se determina en base al factor que se obtiene de la tabla V y es función de la relación X/R.
Tabla V - Valores del factor k y kÖ 2
| X/R | 1 | 1.5 | 2 | 3 | 4 | 5 | 6 | 8 | 10 | ³ 14 |
| k | 1.07 | 1.16 | 1.24 | 1.38 | 1.48 | 1.55 | 1.61 | 1.68 | 1.74 | 1.80 |
| kÖ 2 | 1.51 | 1.64 | 1.76 | 1.95 | 2.09 | 2.19 | 2.27 | 2.38 | 2.46 | 2.55 |
hechas estas determinaciones se dispone de todos los valores que caracterizan la corriente de cortocircuito.
Determinación de la temperatura máxima del conductor
Se puede suponer que antes del cortocircuito el transformador se encuentra en su condición de carga nominal.
Como la norma fija algunas condiciones límites, se puede suponer que la temperatura inicial del devanado es la ambiente (40 °C) más la sobreelevación del conductor correspondiente a la clase de aislación (para Clase A por ejemplo 65 °C) y el objetivo del cálculo es determinar la temperatura final para cierta duración de la corriente de cortocircuito.
La temperatura final J1 de acuerdo con la IEC 76-5 Amend 2 @ (1994) resulta:
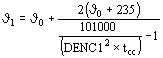°C (cobre)
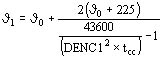°C (aluminio)
siendo:
J0: temperatura inicial del conductor
DENC1: densidad de corriente en cortocircuito A/mm2
tcc: duración del cortocircuito seg.
Estos cálculos deben realizarse para cada uno de los distintos devanados, debiéndose controlar finalmente que no se excedan los valores de J2.
Tabla III - Valores máximos de la temperatura media de devanados después de un cortocircuito J2
| Tipo de transformador | Temperatura de la clase de asislació | Valor de J2 | |
| Cobre | Aluminio | ||
| Inmerso en aceite | A | 250 ºC | 200 ºC |
| Secos | A E B F y H |
180 ºC 250 ºC 350 ºC 350 ºC |
180 ºC 200 ºC 200 ºC ¾ |
Por razones didácticas, y siendo un antecedente de interés que se utilizó durante varios años se transcribe la modalidad indicada en la IEC 76-5 (1976).
La temperatura final J1 es:
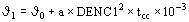°C
siendo:
J0: temperatura inicial del conductor °C
DENC1: densidad de corriente en cortocircuito A/mm2
tcc: duración del cortocircuito seg.
a: factor auxiliar
La densidad de corriente que interesa para el cálculo es la que corresponde al arrollamiento en cortocircuito que se analiza, y puede obtenerse a partir de la densidad de corriente correspondiente a la potencia nominal por la relación entre la corriente nominal y la de cortocircuito.
Según el material con que está construido el devanado cobre o aluminio, se determina un factor auxiliar que depende del calor específico, densidad y resistividad, que varía con la temperatura.
Este factor se encuentra en la tabla IV de la norma, y es función de la temperatura media Jm y del material.
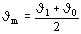°C
La Tabla III fija los valores máximos permisibles de JL según el tipo de transformador, clase de aislación y material del conductor.
Para calcular el valor de "a" es necesario conocer J1 temperatura final que es incógnita, esto puedehacerse en forma iterativa, partiendo de un primer valor de J1 se determina a y con él se calcula un mejor valor de J1 hasta lograr un resultado satisfactorio.
Este cálculo supone que el proceso de calentamiento del conductor durante el cortocircuito es un fenómeno adiabático, es decir que todo el calor producido por la corriente incrementa la temperatura del conductor
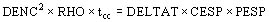
siendo:
DELTAT: incremento de temperatura por la corriente de cortocircuito
CESP ´ PESP: calor especifico por densidad
DENC: densidad de corriente A/mm2
RHO: resistividad media para el salto de temperatura W mm2/m
tcc: duración del cortocircuito seg
El valor de J1 no debe superar los límites de la tabla III según el tipo de transformador, clase de aislamiento y material conductor.
Otro problema puede ser determinar la duración del cortocircuito que haga se alcance la temperatura límite, en este caso el cálculo es inmediato.
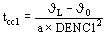seg
Esfuerzos electrodinámicos
Para que un transformador sea capaz de superar con éxito los esfuerzos de este tipo que se pueden presentar durante su vida, es necesario:
- un buen diseño.
- verificación por medio del cálculo y de ensayos.
- un adecuado programa de control de calidad de los materiales utilizados.
- y control del proceso de fabricación de los componentes y de su montaje.
Se destaca que sólo el buen diseño y verificación de cálculo no dan suficiente garantía, son indispensables por ejemplo el control de las características físico químicas de los materiales conductores y aislantes, el control de fabricación de los arrollamientos durante su elaboración y armado final, y de los procesos de secado, estabilización, impregnación, etc. y finalmente proceder a un adecuado mantenimiento.
En este trabajo se describe una metodología simplificada para calcular las solicitaciones de los arrollamientos sometidos a estos esfuerzos.
Además se señala la orientación para efectuar estudios más rigurosos para mejorar el conocimiento de estos fenómenos y evaluar cuantitativamente sus consecuencias.
Los ensayos de laboratorio son los que finalmente permiten verificar la validez de los modelos adoptados en los cálculos, y en consecuencia realimentar la experiencia de quien realiza este tipo de trabajos.
Las normas también establecen las condiciones que deben cumplir los transformadores con relación a estos ensayos.
Es necesario disponer de métodos de cálculo por lo siguiente:
como medio de comparación entre valores calculados y resultados de ensayo
para los casos en que no es posible efectuar ensayos de cortocircuito, es decir sobre todo para transformadores mayores que las posibilidades de ensayo
Características mecánicas de los materiales conductores
Los materiales normalmente utilizados en la construcción de los devanados de los transformadores son el cobre y el aluminio, estos materiales pueden ser recocidos o endurecidos por elaboración en frío.
Las normas indican para cada tipo de material los valores de resistividad que no deben superarse para una temperatura de referencia, para garantizar la calidad del material.
El módulo de elasticidad E y la carga límite de fluencia s D son las características que se requieren conocer para la determinación de la resistencia mecánica de los metales a esfuerzos.
La característica deformación en función de la carga para el cobre y el aluminio se apartan gradualmente de la linealidad, no estando bien definidos los límites de proporcionalidad y de fluencia (como ocurre con el hierro).
Por esta razón se adopta como límite de fluencia la carga para la cual corresponde una deformación permanente igual a 0.2 % de la longitud inicial de la probeta, y se lo denomina s 0.2 (kg/mm2).
La deformación está dada por la relación
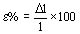
y el módulo de elasticidad
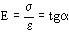
La figura 770 muestra el significado de estos parámetros.
El límite de fluencia está relacionado con los siguientes factores:
- a. Endurecimiento debido a la elaboración en frío. En estas condiciones para el cobre el valor de s 0.2 puede ser aumentado de 4 kg/mm2 (material recocido) hasta 40 kg/mm2, análogamente para el aluminio se pasa de 1.8 kg/mm2 a 17 kg/mm2.
- b. El valor de s 0.2 disminuye con el aumento de la temperatura, por ejemplo pasando de 20 °C a 105 °C se tiene una reducción del orden del 10 %.
- c. La aleación con otros metales (por ejemplo un 0.04 % de plata en el cobre, para el aluminio el contenido de cobre no debe ser mayor de 0,05 % y de cobre más silicio más hierro no mayor de 0,5 %) puede mejorar s 0.2 sin empeorar la conductibilidad.
Características mecánicas de los materiales aislantes
Los materiales aislantes más utilizados en la elaboración de los devanados de grandes transformadores son el papel tipo kraft con una densidad del orden de 0.75 a 0.85 kg/dm3, con espesor típico de 0.5 mm, y el transformerboard para la elaboración de cilindros de soporte, distanciadores, listones separadores etc. es normalmente de tipo duro, prensado en caliente, con una densidad del orden de 1.25 kg/dm3 y distintos espesores.
En máquinas de menor tamaño se usan otros materiales aislantes de menor jerarquía, y la madera.
Puesto que los conductores son mucho más rígidos que el papel y el transformerboard el comportamiento de los arrollamientos sometidos a las fuerzas axiales de cortocircuito está definido por la respuesta de los aislantes a los esfuerzos de compresión.
En los diagramas de deformación en función de la carga, que representan la característica mecánica más importante de los aislantes, se puede observar como se comportan y evaluar su conducta frente a un cortocircuito.
Al examinar estos diagramas es necesario considerar los casos de carga estática y dinámica.
Carga estática
Se presenta cuando un arrollamiento se somete a la compresión constante o bien variada pero en forma relativamente lenta. Esto ocurre durante el tratamiento y montaje de los arrollamientos.
Si un arrollamiento estabilizado (sometido en forma lenta a la compresión y secado antes de ser montado), se lo somete a ciclos sucesivos durante los cuales la presión supera el valor máximo de estabilización, se verifican ulteriores deformaciones permanentes y es necesario repetir 3 a 4 ciclos para obtener una nueva estabilización.
El estado en cual queda el arrollamiento que ha sido sometido a este tratamiento se lo denomina precompresión.
La determinación de las características mecánicas de los materiales aislantes, es decir, la característica deformación en función de la carga, es un problema muy importante. Los resultados obtenidos por distintos investigadores son bastante discordantes.
Estas diferencias se deben al hecho que los resultados experimentales dependen de numerosos factores, siendo los más importantes:
- El tratamiento preliminar del prototipo (presión, temperatura, etc.)
- Dimensiones del prototipo y cantidad de capas
- Terminación de la superficie
- Duración de aplicación de la carga
- Temperatura de la prueba
Si se dispone de los diagramas para el papel e 1 = f (s ) y para el transformerboard e 2 = f (s ) se puede durante el proyecto estimar las deformaciones estáticas de un devanado cualquiera.
Siendo en efecto los conductores mucho más rígidos que los materiales aislantes, su deformación se puede despreciar y por lo tanto para la deformación de un devanado sometido a la compresión se tiene:
D H = D H1 + D H2
siendo D H1 y D H2 la deformación del papel y del transformerboard respectivamente.
Por otro lado se tiene:
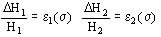
donde H1 y H2 son el espesor total de papel y el espesor total de transformerboard en el sentido axial del arrollamiento.
Para un valor de la carga s de los diagramas correspondientes se tienen los valores de e1 y e2 y con ellos se calcula el valor de la deformación total del devanado.
Para tener una cierta precisión se debe tener en cuenta para el cálculo de DH la disminución de volumen debido al proceso de secado, las deformaciones permanentes provocadas por los ciclos de estabilización y el efecto de rozamiento.
Carga dinámica
La carga dinámica se presenta durante el cortocircuito de un transformador, también cuando se producen sobrecargas de importancia y durante una energización (corriente de inserción).
Los conductores del devanado están sometidos a una fuerza mecánica que es proporcional al cuadrado de la corriente, que se tiene en el caso más desfavorable (máxima asimetría).
Las figuras 771 y figura 772 muestran la variación de la corriente y de las fuerzas actuantes en función del tiempo, observándose en la corriente la componente unidireccional (continua), que se extingue en breve tiempo.
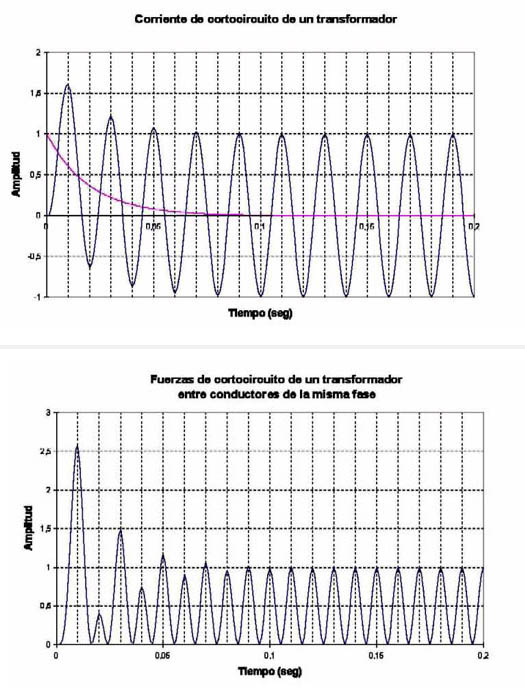
Para las fuerzas (supuestas proporcionales al cuadrado de la corriente) existen dos componentes variables, una de la misma frecuencia que la corriente que desaparece con la componente continua, y la otra permanente con frecuencia doble.
Estas componentes aplicadas sobre los conductores provocan esfuerzos y vibraciones.
Esfuerzos, y vibraciones pueden presentarse en forma radial y axial.
El análisis de las vibraciones axiales se puede realizar considerando un sistema de masas y resortes como se indica en la figura 773. Las masas representan los conductores y los resortes los aislantes.
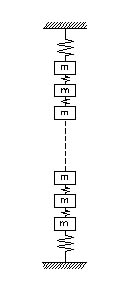
La representación de los materiales aislantes con resortes es posible aunque ellos sólo pueden transmitir esfuerzos de presión y no de tracción, porque los arrollamientos están sometidos a una cierta presión de sujeción que da un estado de precompresión.
Entonces las vibraciones de los conductores provocan aumentos y reducciones de la compresión de los aislantes sin solicitarlos a la tracción.
Si en algunos puntos del arrollamiento la reducción de la presión supera el valor de la compresión se producen separaciones entre conductores y distanciadores.
Para evaluar la respuesta del sistema vibratorio a las fuerzas de cortocircuito, es necesario conocer la característica de los resortes, es decir los diagramas de deformación en función de la carga de los aislantes en condiciones dinámicas.
Estos diagramas no son lineales y no son iguales a aquellos obtenidos para las cargas estáticas.
La figura 774 muestra que por encima del punto de precompresión, en condiciones dinámicas el transformerboard es más rígido y se deforma menos, por debajo de este punto no hay diferencias entre ambas condiciones.
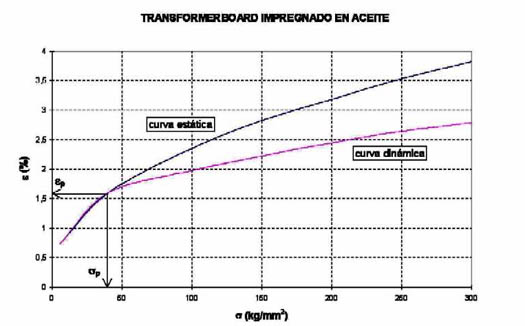
La explicación del comportamiento dinámico del transformerboard se debe a que cuando se le aplica improvisamente una fuerza, el aceite contenido en sus poros está sometido a una presión y tiende a salir. El recorrido del aceite es a través de una estructura capilar y se realiza en forma lenta, por lo tanto durante el tiempo breve transcurrido hasta que la fuerza alcanza su primer pico, el aceite queda atrapado y debido a su alta constante elástica confiere rigidez al transformerboard.
Cuando en cambio la fuerza aplicada reduce la precompresión la presión del aceite retorna al valor inicial, y como no puede transmitir esfuerzos de tracción, la rigidez es solamente la propia del transformerboard.
Se supone que la principal flexibilidad del sistema corresponde al transformerboard (y el papel, pero su influencia es mucho menos importante que la del transformerboard puesto que los espesores de papel son relativamente pequeños).
Campo magnético de dispersión y esfuerzos resultantes
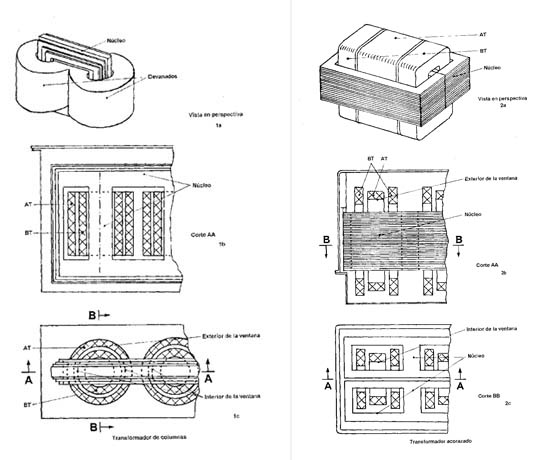
Se distinguen dos tipos de transformadores, de columnas (figura 785A), acorazados (figura 785B), y en cada uno se presentan campos de distinta forma y en consecuencia los esfuerzos resultantes difieren.
Los arrollamientos de un transformador están ubicados en su propio campo magnético de dispersión. Debido a la ley de Amper cada elemento rectilíneo de conductor de longitud dl recorrido por una corriente i, ubicado en un campo magnético de inducción B, está sometido a una fuerza elemental.
dF = i dl B
entendiéndose que la fuerza es el producto vectorial de i dl por B, resultando la fuerza perpendicular al plano formado por el elemento conductor y la inducción magnética.
De aquí surge que las fuerzas se incrementan con las corrientes, interesan los efectos de las fuerzas máximas y por eso deben de tenerse las fuerzas máximas.
Frecuentemente cuando se habla de los esfuerzos electrodinámicos en los transformadores se dice que son proporcionales al cuadrado de la corriente, esta verdad merece un cuidadoso análisis para no degenerar en una idea equivocada.
Esta idea surge de considerar que cuanto mayores son las corrientes mayores son los esfuerzos, mientras que lo que debe observarse es el producto Bi.
Observemos un conductor de un arrollamiento de un transformador, queremos determinar la fuerza que se presenta sobre él. Es necesario determinar el campo B debido a todos los otros conductores, existentes en los arrollamientos, en el lugar ocupado por el conductor de nuestro interés.
Este campo depende del producto del número de conductores por la corriente, y de la distancia entre cada conductor y el punto que estamos considerando.
Para una misma forma constructiva que se aplica a máquinas semejantes dentro de una determinada gama de potencias, al aumentar la corriente aumenta la sección de los conductores y su momento resistente, las tensiones mecánicas dependen de la relación entre la fuerza y el momento resistente, es entonces imposible a priori indicar cual es la potencia a la que corresponden las solicitaciones críticas.
El caso extremo se presenta en transformadores para aplicaciones especiales que manejan corrientes del orden de 50000 A o más, y sólo tienen dos o tres espiras de una sección muy grande, consecuentemente con solicitaciones mecánicas muy bajas.
La determinación de la fuerza se puede hacer con una fórmula simple que sólo es aplicable en el centro del arrollamiento (cuando este es uniforme).
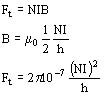
En la figura 786 se muestra para un transformador de columnas el campo axial y las fuerzas radiales en el centro de los arrollamientos.
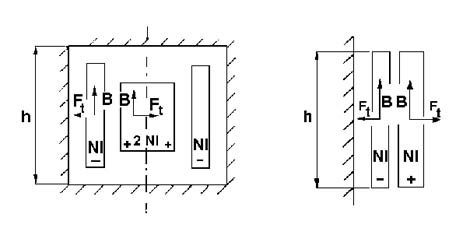
Para un transformador acorazado en el centro de los arrollamientos se observa el campo radial y las fuerzas axiales.
El campo magnético de dispersión de un transformador a columnas de dos arrollamientos concéntricos donde los amper espiras están uniformemente distribuidos y equilibrados, es axial a lo largo de la mayor parte de la altura.
El campo magnético axial produce fuerzas radiales que tienden a abrir el devanado externo y en cambio a aplastar sobre la columna el interno.
Este campo diverge en ambas extremidades y la inducción se puede descomponer en una componente axial Ba, y una componente radial Br.
Las fuerzas axiales en cambio tienen el mismo efecto en ambos arrollamientos tendiendo a comprimirlos hacia el centro.
Esto es así solamente cuando los dos arrollamientos están perfectamente alineados y con una distribución uniforme de los amper espiras.
Cualquier desequilibrio de los amper espiras provocado por perturbaciones locales de la inducción magnética (debidas a desuniformidades, huecos por ejemplo) produce una componente radial de la inducción en esa zona.
Cuando los arrollamientos no están alineados, la distribución de las fuerzas radiales permanece casi invariable, mientras que la distribución de las fuerzas axiales varía y las fuerzas resultantes tienden a aumentar el desequilibrio.
Se destaca que el estudio de la distribución del flujo de dispersión es de fundamental importancia en el diseño un transformador.
Su trayectoria tiene notable incidencia en las pérdidas adicionales, en la presencia de sobreelevaciones de temperatura locales y además en los esfuerzos que se presentan en los devanados debido al cortocircuito.
Esto ocurre particularmente en los extremos de los devanados, y para guiar el campo magnético de dispersión se utilizan piezas magnéticas que se colocan en la zona de los prensayugos y pantallas magnética en la cuba.
En síntesis la distribución de las fuerzas de cortocircuito depende de la disposición y de las dimensiones de los arrollamientos y de la distribución de los amper espiras.
Los arrollamientos se subdividen en un cierto número de elementos, al límite cada conductor puede ser un elemento.
Para cada elemento se determinan los valores de las componentes de la inducción Ba y Br, y conocidos estos valores se calculan las fuerzas elementales que actúan sobre cada conductor.
Un conductor cualquiera está sometido a la suma de dos tipos de esfuerzos:
- El esfuerzo electrodinámico propio, debido a la inducción magnética presente en el lugar en que está ubicado.
- El esfuerzo que experimenta debido a la acción que sobre él hacen los conductores vecinos.
Se determina la componente radial de la inducción magnética para el arrollamiento externo, a lo largo de su altura, esta componente radial produce una fuerza axial que actúa sobre cada conductor.
Como cada conductor transmite fuerza al vecino, la fuerza acumulada es la suma (integral) de las fuerzas elementales (proporcional a la componente radial de la inducción).
La figura 787 representa el caso de arrollamientos simétricos con respecto al plano medio, para los cuales los amper espiras están uniformemente repartidos y equilibrados.
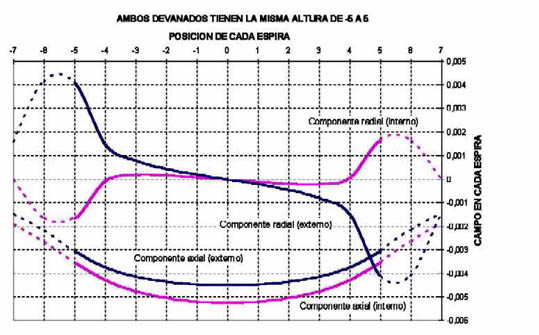
El devanado externo está sometido a esfuerzos de compresión axial que alcanzan el valor máximo en el plano medio de los arrollamientos.
Los esfuerzos aplicados en la mitad superior del arrollamiento están en equilibrio con los aplicados en la mitad inferior.
Si se trabaja con fuerzas finitas (en lugar de infinitesimales) se debe pensar en acumular fuerzas iniciando en ambos extremos y terminando en el centro.
En rigor cuando se acumulan fuerzas se las debe sumar partiendo de un extremo, y siguiendo el sentido de las fuerzas aplicadas, de manera de observar como cada conductor carga al contiguo.
La figura 788 representa el caso de arrollamientos donde los extremos inferiores están alineados, pero el arrollamiento exterior es más bajo que el interior, por lo que en los extremos superiores están desalineados.
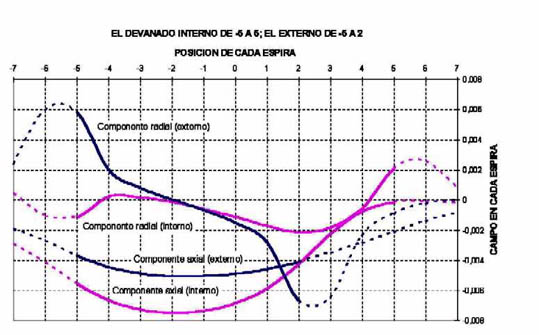
Los amper espiras están siempre uniformemente distribuidos en cada arrollamiento. La componente radial de la inducción magnética correspondiente al arrollamiento externo es mayor en la parte superior del mismo. La curva integral no es más simétrica, y el arrollamiento exterior está sometido, además de un esfuerzo de compresión axial, a un esfuerzo de empuje hacia abajo. Por reacción el arrollamiento interior está sometido a un esfuerzo de empuje hacia arriba.
Debido a este fenómeno, que tiende a que los devanados se muevan axialmente, se presentan esfuerzos de reacción sobre los elementos de sujeción axial, que deben estar realizados para soportarlos.
Este efecto también se presenta en devanados de igual altura cuando hay pequeñas imperfecciones de montaje.
Debe observarse que cuando se inicia dicho movimiento axial la fuerza de repulsión entre devanados tiende a incrementarse por lo que esta situación lleva a la rotura, al colapso.
La figura 789 muestra que la componente radial externa varía entre valores extremos para cada una de las dos galletas que forman el devanado.
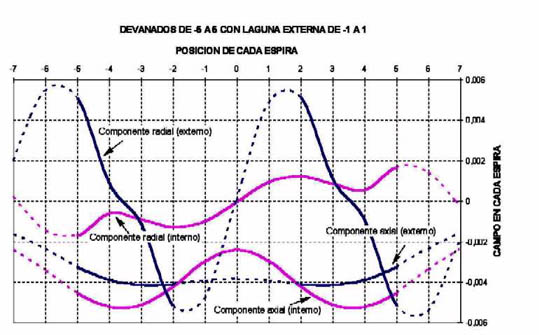
También en este caso, la integral de estas fuerzas nos da como resultado un empuje sobre los elementos de sujeción de las galletas, que tienden a ser expulsadas respecto del plano de simetría.
Límites del estudio - Comportamiento estático y dinámico
Un análisis simplificado considera las fuerzas estáticas aplicadas, pero los esfuerzos electrodinámicos propiamente dichos son una parte de los esfuerzos aplicados a los conductores durante un cortocircuito. Se deben considerar además las fuerzas debidas a:
- La gravitación (masa de los conductores)
- La inercia de los conductores
- La elasticidad de los materiales aislantes
- El rozamiento entre los conductores y sus aislantes
Considerar todo esto complica notablemente el tratamiento, acerca de estos temas se han realizado numerosos estudios teóricos y experimentales que han conducido a calcular las frecuencias propias mecánicas de los arrollamientos.
En estos estudios se deben tener en cuenta muchos parámetros constructivos propios de cada construcción, donde los valores exactos son muy difíciles de acertar.
En un transformador a columnas, las características mecánicas de un arrollamiento de capas (generalmente de baja tensión) son muy diferentes de aquellas de un arrollamiento de discos (generalmente de alta tensión), no se puede decir a priori cual está más exigido, cual es más probable falle.
Para un arrollamiento de capas la relación entre el espesor total de los aislantes y el espesor del conductor es sensiblemente menor en el sentido axial que en el sentido radial, en cambio en el arrollamiento de discos, debido a la presencia de los canales radiales esta relación es inversa.
En un arrollamiento de capas, por lo menos un lado de cada capa está en contacto directo con el aislante en toda su superficie. Las fuerzas axiales de rozamiento resultan grandes, a la inversa en los arrollamientos de discos donde los distanciadores radiales recubren una pequeña parte de la superficie lateral.
Además para arrollamientos del mismo tipo, el coeficiente de elasticidad de los aislantes depende no solamente de los materiales utilizados, sino también, en gran medida, del tratamiento térmico a que están sometidos los arrollamientos antes del montaje y finalmente con el transformador completo.
En cuanto a las fuerzas de rozamiento, ellas dependen de la cantidad y de la superficie de los distanciadores radiales y axiales, de la manera como ha sido ajustado el arrollamiento durante su fabricación, de su compacticidad después del tratamiento térmico del transformador.
Finalmente la naturaleza de los dispositivos de sujeción axial y los valores de precompresión aplicados a los arrollamientos modifican igualmente, en grandes proporciones, la elasticidad de los aislantes y por lo tanto los valores de frecuencia natural.
Teniendo en cuenta la cantidad de parámetros a introducir, y la imposibilidad de definir para cada uno de ellos los valores aceptables para todas las construcciones, se aceptan frecuentemente algunas hipótesis simplificativas en los métodos de cálculo para aplicarlos a todos los tipos de transformadores y, con este objetivo, se desprecian las fuerzas debidas a la inercia de los conductores, a la elasticidad de los aislantes, y al rozamiento de los conductores con los aislantes.
Con estas hipótesis simplificativas el estudio queda reducido a realizar solamente cálculos estáticos de los esfuerzos electrodinámicos propiamente dichos.
En los transformadores monofásicos los cálculos se realizan para el mayor valor de cresta asimétrica de la corriente.
En los transformadores trifásicos se considera el instante en que en una fase alcanza el mayor valor de cresta asimétrica, y en las otras dos el valor es la mitad y opuesto.
Modos de aflojamiento de los devanados
Pensemos en ensayos, en los cuales observamos consecuencias de los esfuerzos, que son deformaciones, y a través de ellos tratamos de comprender las causas, los esfuerzos, y como se debe encarar el problema para lograr resolverlo.
Las elevadas fuerzas electrodinámicas asociadas a las corrientes de cortocircuito pueden llevar a deformaciones elásticas de la estructura o bien deformaciones permanentes, estas últimas más o menos graves y extensas.
Se distinguen:
Aflojamientos por fuerzas radiales, causadas por:
- Aflojamiento de conductores en los arrollamientos externos por solicitaciones a tracción que exceden el límite de fluencia del material.
- Deformación permanente del arrollamiento interno, los conductores se pliegan y el devanado adopta una forma característica denominada estrella de mar, debido a que los esfuerzos son elevados.
- Colapso del arrollamiento interno por inestabilidad de forma pandeo (conocida como "buckling" del inglés o "flambage" del francés) debido a la debilidad estructural.
Aflojamientos por fuerzas axiales, causadas por:
- Inclinación de los conductores (conocida como "tilting" del inglés), favorecido por un reducido espesor de las planchuelas y escasa adherencia entre conductores adyacentes.
- Aflojamientos de las estructuras aislantes de los extremos de los arrollamientos (anillos, bloques distanciadores, etc.) por debilidad intrínseca, o bien por desplazamiento o desalineamiento de los elementos de soporte.
Aflojamientos en puntos singulares tales como:
- Puentes internos o externos, transposiciones de los conductores, pasaje de un conductor de un estrato a otro adyacente, tomas de conexión a los conmutadores, terminales de arrollamientos, etc. El aflojamiento puede deberse a debilidad estructural o insuficiente soporte o fijación.
Los aflojamientos de las máquinas debido a un cortocircuito implican daños muy grandes.
La magnitud de los daños, la gravedad de la salida de servicio en forma imprevista, los costos de las reparaciones y los largos tiempos de indisponibilidad de las máquinas conducen a buscar siempre mayor confiabilidad adoptando para ello las siguientes acciones:
- Mejorar la concepción, el proyecto y la construcción de las máquinas.
- Verificar la capacidad de soportar estos esfuerzos con pruebas de cortocircuito.
- Efectuar sistemáticamente controles de diagnóstico en las máquinas en servicio.
Fuerzas de cortocircuito y su distribución en los devanados
Fuerzas radiales
Los devanados internos son más críticos para soportar los esfuerzos radiales, debido a que en ellos puede manifestarse el colapso por inestabilidad de forma (pandeo).
Estos arrollamientos se apoyan en un conjunto de listones uniformemente distribuidos, se puede suponer cada tramo de arrollamiento como una viga (continua) con carga uniforme, que están soportados por un cilindro de material aislante (distanciador) que circunscribe el núcleo. Este cilindro a su vez está apoyado mediante un conjunto de listones de centrado sobre el núcleo.
En el caso de que este devanado tenga canales axiales de refrigeración las espiras externas de la última capa (exterior) que son las más solicitadas (campo de dispersión máximo) se descargan sobre las capas más internas.
Cuando no se requiere ningún canal de refrigeración (devanado tipo hélice), se realiza directamente sobre un tubo soporte de material aislante que está apoyado sobre el núcleo mediante listones de centrado.
El esfuerzo radial total o parcial se descarga siempre sobre estos apoyos y por lo tanto para el cálculo de los esfuerzos se considera siempre como una viga empotrada (continua).
El problema de diseño consiste en determinar el número mínimo de distanciadores necesarios (luz de la viga) para garantizar la resistencia requerida.
Las dos posibilidades de deformación para el arrollamiento interno son la estrella de mar o el pandeo, la figura 790 muestra estos ejemplos.
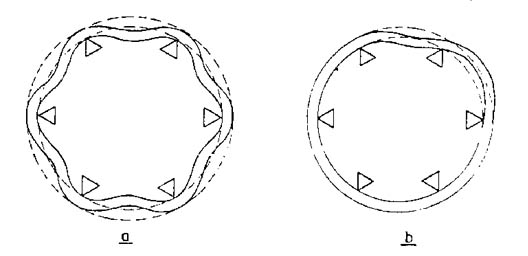
En un devanado externo sin canales de refrigeración, las espiras de la primera capa (interior) que son las más solicitadas (campo de dispersión máximo) se descargan sobre las capas más externas menos solicitadas.
Si el devanado tiene canales de refrigeración que dividen el arrollamiento en secciones, los esfuerzos de las espiras internas se descargan sobre las espiras externas a lo largo de los distanciadores verticales.
Entre dos distanciadores las espiras internas se comportan como una viga cargada uniformemente y solicitada a la flexión. Dependiendo del tipo de apoyo la viga se puede considerar empotrada en ambos extremos o bien una viga continua.
Fuerzas axiales
En un punto anterior se analizaron distintos casos de arrollamientos uniformes, con distinta altura y con lagunas y su efecto en las fuerzas axiales.
La dirección de las fuerzas actuantes durante el cortocircuito depende de la disposición y de la distribución de los amper espiras.
Cabe destacar que los cálculos que se pueden realizar, son válidos para las disposiciones simples citadas, no así cuando se trata de devanados múltiples o con muchas lagunas.
Las fuerzas axiales pueden provocar que un arrollamiento de discos ceda debido a una brusca inclinación de los conductores como muestra la figura 791.
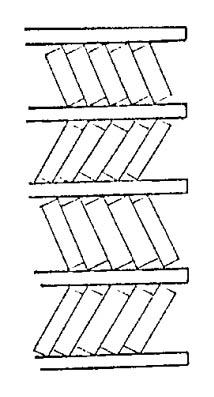
Esta inclinación ("tilting") se puede presentar en uno o más discos de un arrollamiento, y se debe a que las fuerzas axiales que se transmiten a través de los distanciadores pueden no estar centradas, en esas condiciones aparecen momentos que tienden a inclinar los conductores.
Tensiones mecánicas en los conductores debidas a los esfuerzos de cortocircuito
La elección del tipo de devanado (hélice, discos) está condicionada por el número de espiras y por la corriente.
A modo orientativo los devanados que tiene muchas espiras y bajas corrientes serán del tipo a discos, en cambio arrollamientos con pocas espiras y altas corrientes se eligen preferiblemente de tipo hélice.
Un arrollamiento a discos está formado por galletas en serie.
Llamamos galleta a un devanado de tipo concéntrico continuo que puede tener una o más capas y cada capa puede estar constituida por una o más espiras.
En el caso particular de tener una galleta una sola espira por capa y varias capas la llamamos disco.
A continuación se examinan solamente los arrollamientos a disco, sin embargo las conclusiones se pueden extender a otros tipos de arrollamientos.
En la figura 793 se indican detalles constructivos de un arrollamiento a disco.
Para la determinación de las tensiones mecánicas en los conductores debido a las fuerzas de cortocircuito, se realizan las siguientes hipótesis simplificativas:
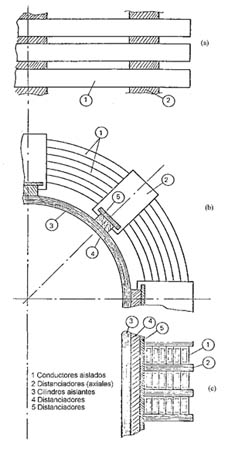
- a. Los conductores de cada disco se consideran como un sistema de anillos concéntricos.
- b. La relación entre el espesor y el radio de cada anillo es pequeña y por lo tanto la distribución de las tensiones de tracción y compresión en la sección de un conductor se puede considerar constante.
- c. El material conductor se lo utiliza en la parte lineal de la característica deformación - carga, por lo tanto es aplicable el principio de superposición de los efectos, siendo posible estudiar separadamente la acción de las fuerzas radiales y axiales superponiendo sus resultados.
- d. La distribución de fuerzas se considera uniforme a lo largo de la circunferencia de cada conductor.
- e. La frecuencia propia de los arrollamientos para las vibraciones axiales y radiales está lejos de la correspondiente a las fuerzas de cortocircuito, por lo tanto se descarta la posibilidad del fenómeno de resonancia.
Se pueden aplicar por lo tanto las fórmulas para una carga estática.
Cargas del arrollamiento externo
Como se observa en la figura 794 cada conductor está sometido a cargas específicas radiales p y axiales q.
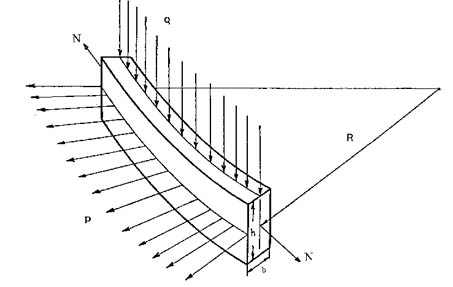
Bajo el efecto de la carga radial p cada conductor del disco considerado se deforma aumentando su radio.
En las zonas correspondientes a los distanciadores axiales, estas deformaciones radiales están impedidas solamente por el rozamiento del aislamiento de papel de los conductores y el transformerboard de los distanciadores figura 793 (c).
Debido a las vibraciones durante el cortocircuito, la presión axial que actúa sobre los distanciadores varía y por lo tanto también este rozamiento.
Este vínculo resulta inseguro y por simplificación del cálculo se lo desprecia.
Como se observa en la figura 794 el conjunto de fuerzas radiales p se encuentra en equilibrio con las fuerzas N (de tracción) que son iguales por razones de simetría, es decir la carga radial provoca una solicitación de tracción, siendo la tensión correspondiente igual a:
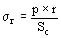
siendo Sc la sección del anillo (conductor).
Para cada conductor el valor de p es distinto. La distribución de p se indica en la figura 795 y la de la inducción B en la figura 796.
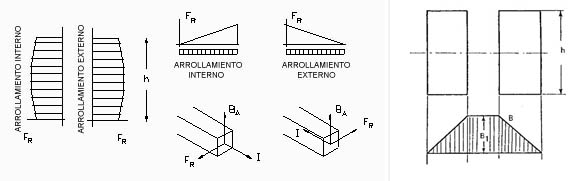
Las deformaciones radiales varían de un anillo al otro comprimiendo el aislamiento (papel). El aislamiento transfiere parte de la carga de un conductor al otro, de este modo se produce una redistribución de los esfuerzos haciéndose más pareja la carga en los conductores.
Esta redistribución requiere el conocimiento de datos que no siempre están disponibles. En algunos casos desfavorables esta redistribución difiere poco de la distribución de p (prácticamente no hay distribución).
En este caso el cálculo de la tensión interna se simplifica notablemente porque la carga de cada anillo se conoce y es suficiente considerar solamente el anillo más solicitado (el interno).
Para estas condiciones la carga específica radial resulta:
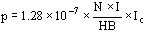(kg/mm)
siendo NI la fuerza magnetomotriz, HB la altura del devanado y Ic la corriente en el conductor.
El valor máximo de esta carga específica p se encuentra en la mitad de la altura del arrollamiento.
El efecto de la carga axial q en un anillo que tiene distanciadores radiales para formar los canales radiales de refrigeración, se manifiesta como una flexión en el tramo comprendido entre dos distanciadores.
Se puede considerar este tramo de conductor como una viga empotrada en ambos extremos (viga continua), esta suposición se justifica por razones de simetría y por tratarse de una estructura anular continua.
Debido a la presencia de la componente radial del campo magnético, sólo hay fuerza axial en los extremos de cada arrollamiento. Pero además a medida que se pasa del interior al exterior del arrollamiento la fuerza axial varía en la misma forma en que aumenta la inducción magnética radial.
La figura 797 muestra la distribución de esta solicitación donde se observa que el valor máximo se tiene hacia la mitad del espesor del disco.
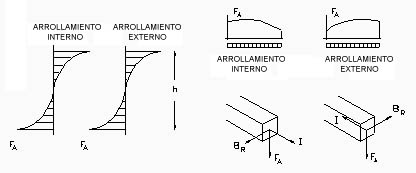
Normalmente para los cálculos se adopta un valor medio de q. Esta simplificación es aceptable debido a que el valor máximo de q no se presenta en el mismo punto que el valor máximo de p.
Para evaluar el efecto de la carga axial se supone rectilíneo el tramo de conductor sin cometer errores apreciables (momento de torsión despreciable), debido a que los radios y el número de distanciadores son tales que hacen pequeña la diferencia entre la cuerda y el arco.
La figura 798 muestra el diagrama de carga axial q (uniformemente distribuida), el diagrama de momentos y el diagrama de solicitación tangencial (corte), observándose que las máximas solicitaciones (momento flector y corte) se tienen en los extremos de la viga.
Las solicitaciones a flexión y tracción están en equilibrio con las tensiones internas sa y ta, actuando la tensión sa normal a la sección del conductor y con una distribución como se indica en la figura 799 (b).
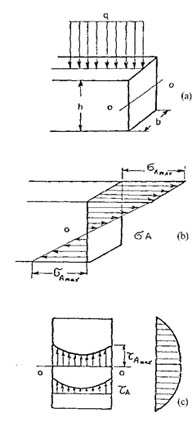
Su valor máximo se tiene en los puntos más alejados del eje neutro y resulta:
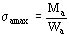(kg/mm2)
siendo Ma el momento flector y Wa el módulo resistente de la viga que por tratarse de una sección rectangular resulta:
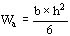
La sección más solicitada se encuentra en el extremo de la viga donde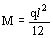 
por lo tanto:
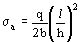
La tensión tangencial ta actúa en el plano de la sección y su distribución se indica en la figura 799 (c), su valor máximo se encuentra en el eje neutro y en correspondencia con los bordes.
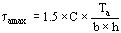
siendo C un factor que depende de la relación b/h y del coeficiente de Poisson que relaciona, dentro del período elástico, la variación unitaria de dimensión en el sentido transversal con la longitudinal. La tabla muestra algunos valores de C, considerando el coeficiente de Poisson igual a 0.3:
| b/h | 0.5 | 1.0 | 2 | 4 |
| C | 1.033 | 1.126 | 1.396 | 1.988 |
Como visto la carga radial p produce una tensión normal a la sección del conductor sr, y la carga axial en cambio produce una tensión normal s a y una tangencial t a, en consecuencia las tensiones resultantes son:
s = s r + s a t = t a
La tensión máxima de corte ta debida a la carga axial se tiene en el eje neutro, donde la tensión normal debida a la carga axial s a es nula.
Como el valor de s es mucho más grande que el valor t , es suficiente verificar solamente la resistencia a las tensiones normales (en dirección longitudinal).
Se debe cumplir que la tensión normal resultante s sea menor o igual a la tensión admisible para el material de los conductores.
Este último valor se puede definir en base a la deformación permanente de los arrollamientos que se admite, aceptándose como deformación tolerable 0.2 %, y adoptando algún coeficiente de seguridad.
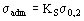
Este coeficiente de seguridad KS fijado por el constructor tiene en cuenta la incertidumbre en la determinación de las características de los materiales, y la tolerancias de fabricación.
En su determinación es necesario además tener en cuenta que la deformación permanente depende del valor pico de la corriente y del número de cortocircuitos soportados (estadísticamente) durante su vida útil (estimada en 20 a 30 años).
Inestabilidad a la compresión axial del arrollamiento externo
Las fuerzas axiales pueden provocar el colapso del arrollamiento debido a una brusca inclinación de los conductores como se puede observar en la figura 791.
Esta inclinación ("tilting") se puede producir en uno o más discos del arrollamiento, y se debe a que las fuerzas axiales que se transmiten a través de los distanciadores pueden no estar perfectamente centradas. En estas condiciones se presentan momentos que tienden a inclinar los conductores.
Para analizar este fenómeno observamos un conductor único que se aproxima a un anillo y que experimenta, por una razón cualquiera, una pequeña inclinación respecto a su posición inicial, figura 800.
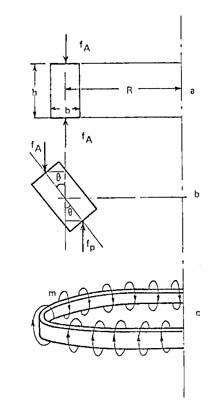
Para simplificar el análisis se supone que todas las secciones del anillo se han inclinado del mismo modo, es decir que el ángulo J es constante a lo largo de la circunferencia del anillo, y las fuerzas fA están uniformemente distribuidas.
El momento por unidad de longitud del anillo resulta:
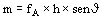
A este momento que tiende a incrementar el ángulo J se oponen otros dos momentos que son mc provocado por la deformación del conductor y md provocado por la deformación de los distanciadores (superiores e inferiores) en los cuales el conductor se apoya.
Estos momentos se calculan con las siguientes expresiones:
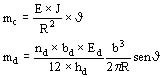
siendo:
nd: número de distanciadores
bd: ancho de los distanciadores
Ed: módulo de elasticidad del distanciador
hd: altura (espesor) del distanciador radial
En condiciones de equilibrio se tiene:
m = mc + md
y cuando m > mc + md el ángulo J aumenta en forma brusca y se produce el colapso del arrollamiento.
El valor crítico de la fuerza axial para un valor de J pequeño y para una sección rectangular (J = bh3/12) resulta:
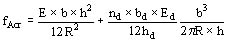
Si el número de conductores en un disco es nc la fuerza axial total crítica resulta:
FAcr = nc ´ 2p R ´ fAcr
en este caso R es el radio medio del arrollamiento.
Esta fórmula es válida si se supone que los distanciadores horizontales no pueden desplazarse, en caso contrario el momento ms resulta nulo y la fuerza fAcr se reduce sólo al primer término.
En estas aproximaciones no se tienen en cuenta el radio de curvatura de los conductores y del aislamiento de papel.
El problema es más complejo, las fuerzas fA no están uniformemente distribuidas, sólo están concentradas en la zona de los distanciadores radiales.
Cargas del arrollamiento interno
La diferencia con el arrollamiento externo es que las fuerzas radiales actuantes tienen dirección opuesta. Cada conductor de un disco del arrollamiento interno está cargado como muestra la figura 801, donde las solicitaciones normales N en este caso son de compresión.
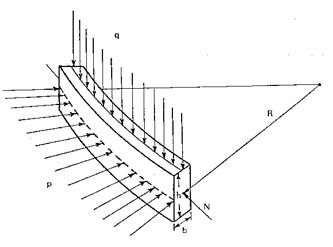
Bajo el efecto de la compresión radial p cada anillo se deforma tendiendo a disminuir su radio.
En su parte interior cada anillo se apoya en un cierto número de distanciadores axiales, realizados con transformerboard o en máquinas de menor potencia con madera, que no siendo totalmente rígidos permiten desplazamientos radiales.
Para un anillo con apoyos la figura 802 muestra parte de un conductor que tiene una carga uniformemente distribuida y que está soportado por distanciadores colocados a distancias iguales.
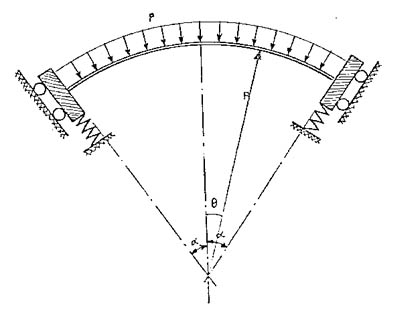
Se trata de un problema estáticamente indeterminado que ha sido estudiado por distintos autores, y se puede demostrar que las solicitaciones en una sección cualquiera de la viga (anillo) resultan:
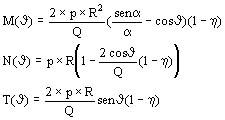
siendo:
J: ángulo (según figura de 0 a a)
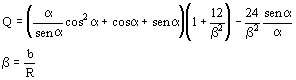
h: es el valor relativo del aflojamiento de los apoyos que vale 0 para apoyos considerados infinitamente rígidos y 1 sin apoyos
Las solicitaciones M, N y T resultan máximas para J = a , es decir en la extremidad de la viga, por lo tanto los cálculos se deben realizar para estas secciones.
Las tensiones tangenciales T(a ) se desprecian debido a que también para este arrollamiento el valor de s resulta mucho más grande que el valor de t , y es suficiente verificar sólo la resistencia a las tensiones normales que resultan:
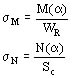
Para los conductores de sección rectangular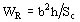 
y Sc = b ´ h.
El valor máximo de la tensión normal es:
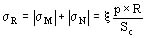
siendo:
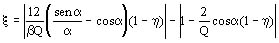
Si no hay apoyos (h=1) resulta x = 1 y por lo tanto resulta:
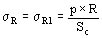
igual a la expresión vista para el arrollamiento externo con la diferencia que la fuerza p es ahora de compresión.
El factor x es función del número de distanciadores y de b que es la relación entre el espesor del conductor y el radio medio del anillo.
La figura 803 muestra para apoyos rígidos (h =0) como varía este factor, observándose dentro de ciertos límites que el aumento del número de distanciadores implica un incremento de las tensiones internas en lugar de una reducción.
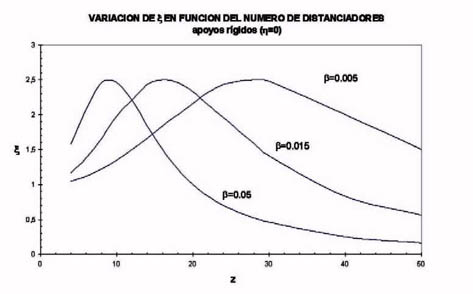
Una explicación física de esta situación se debe a que por un lado con el aumento del número de distanciadores Z se reduce la longitud de la viga y por lo tanto su solicitación, por otro lado el efecto de arco que refuerza la viga disminuye con el aumento de Z (la viga resulta prácticamente rectilínea).
Distintos autores han estudiado el efecto que el número de distanciadores axiales tiene en el valor de las tensiones internas, encontrando que cuanto menos rígidos son los apoyos (el caso límite sin apoyos) menores son las tensiones internas.
En la parte ascendente de las curvas predomina la disminución del efecto de arco mientras que la parte descendente está determinada por la reducción de longitud de la viga.
En base a estos resultados parecería que los apoyos no sirven, pero no es así debido a que la estabilidad a la compresión de un devanado aumenta con el cuadrado de la cantidad de apoyos, siendo este aspecto decisivo para la elección del número de distanciadores a utilizar.
Un anillo sometido a la compresión radial p puede colapsar por inestabilidad (pandeo) de manera similar a como ocurre con una viga cargada de punta.
Como ya visto las tensiones tangenciales se pueden despreciar y por lo tanto las tensiones resultantes se obtienen sumando las tensiones normales debidas a las fuerzas axiales con aquellas debidas a las fuerzas radiales.
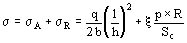
El valor de s así obtenido debe resultar menor al valor admisible para el material del conductor.
Inestabilidad a la compresión radial del arrollamiento interno.
Un anillo sometido a la compresión radial p puede aflojarse por inestabilidad de modo análogo a una viga cargada de punta. Si el esfuerzo de compresión debido a las fuerzas radiales supera un valor crítico, que depende de la forma constructiva de los devanados, se puede producir el colapso por pandeo.
Para un anillo sin vínculos el valor crítico de compresión está dado por:
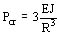
Para un anillo vinculado este valor depende mucho del tipo de vínculos.
Para un arrollamiento interno se presenta una gran incertidumbre acerca del tipo de vínculo a considerar.
Por tal motivo se proponen expresiones del valor crítico de compresión para algunos tipos de vínculos. La elección de la expresión más adecuada se debe realizar en base a resultados experimentales.
A. Vínculos que impiden solamente desplazamiento en sentido radial
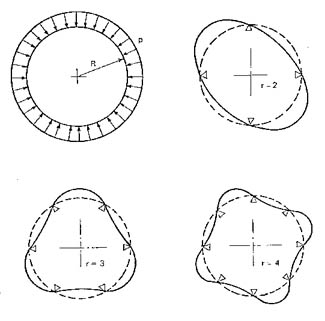
Este caso se lo conoce en la bibliografía como "buckling" o "flambage" donde los conductores se pliegan localmente hacia el interior entre dos soportes axiales adyacentes y hacia el exterior en correspondencia con el siguiente soporte.
Para este caso es válida la expresión:
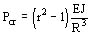
donde r > 2 es el número de ondas completas que se forman a lo largo del perímetro del anillo, en la figura 804 se observan los casos para r = 2, 3 y 4 siendo R el radio interno del anillo.
La relación entre el número de ondas y de vínculos z es:
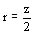
por lo tanto la expresión de la carga crítica resulta:
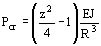
B. Vínculos que impiden solamente rotaciones
En este caso se aplica la fórmula:
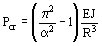
si se desprecia el ancho de los soportes axiales se tiene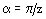 
, y por lo tanto resulta:
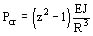
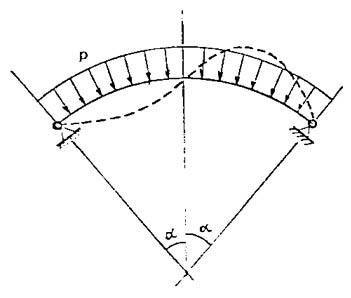
C. Vínculos empotrados
Con ellos se intenta impedir el desplazamiento en sentido radial y las rotaciones.
Este caso se puede presentar probablemente aumentando la presión de sujeción, es decir la compresión axial sobre los distanciadores.
La figura 805 muestra como se produce la deformación del anillo entre dos apoyos que solamente permiten una rotación.
En cuanto a las cargas axiales su efecto es idéntico a lo visto para el arrollamiento externo, pudiéndose aplicar las mismas fórmulas.
Finalmente la tensión resultante s se determina en forma análoga a lo visto para el devanado externo.
Frecuencia propia del arrollamiento externo debido a las vibraciones radiales.
Para estimar la frecuencia propia de un arrollamiento que vibra radialmente se puede utilizar la fórmula correspondiente a un anillo
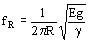
siendo:
R: radio medio del arrollamiento (cm)
E: módulo de elasticidad del conductor (kg/cm2)
g: aceleración de la gravedad 981 cm/s2
g: peso específico del conductor (kg/cm3)
Para el cobre E = 1,06´ 106 kg/cm2 y g = 8,9´ 10-3 kg/cm3
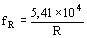Hz
Para el aluminio E = 6,7´ 105 kg/cmv2 y g = 2,7´ 10-3 kg/cm3
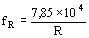Hz
Frecuencia propia del arrollamiento interno por vibraciones radiales
La frecuencia propia de un anillo con apoyos rígidos que vibra radialmente resulta:
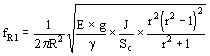
donde r3 2 es el número de ondas completas que se forman a lo largo del perímetro del anillo.
El valor de r depende del número de apoyos Z. Puesto que entre dos apoyos hay un número entero de semiondas para la frecuencia más baja se tiene que R=Z/2.
La expresión anterior se puede simplificar:
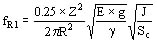
para una sección rectangular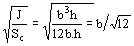 
obsérvese que como se está analizando la vibración radial de los conductores el momento de inercia debe considerarse sobre el eje longitudinal del arrollamiento.
Se tienen respectivamente las siguientes relaciones:
para el cobre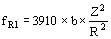 
para el aluminio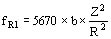 
donde b y R están dados en cm.
Frecuencia propia de los conductores debido a las vibraciones axiales
La frecuencia de vibración fundamental (la más baja) de un viga empotrada está dada por:
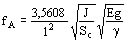Hz
siendo:
J: momento de inercia de la sección de la viga (J = b3h/12) obsérvese que como se está analizando la vibración axial de los conductores debe considerarse sobre el eje paralelo al plano que contiene el anillo
Sc: sección de la viga (Sc = b.h)
l: longitud de la viga (luz) (cm)
b: espesor del conductor (cm)
para el cobre Hz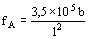 
para el aluminio Hz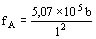 
Vibraciones axiales de los arrollamientos - Frecuencia de resonancia
Como visto el arrollamiento se puede representar como un sistema de masas y resortes. Durante el cortocircuito este sistema es excitado por las fuerzas axiales que varían en el tiempo como indica la figura 772.
La respuesta del sistema depende de la amplitud de estas fuerzas perturbadoras como así también de la relación entre su frecuencia y la frecuencia natural del sistema.
Si las dos frecuencias son iguales se produce resonancia, en este caso se tiene una amplificación de la amplitud de las vibraciones y de la fuerza transmitida a los soportes que pueden alcanzar valores muy altos.
Para el problema de diseño no es imprescindible calcular los esfuerzos resultantes, si en cambio efectuar las acciones necesarias para evitar la resonancia.
Es necesario calcular la frecuencia propia de resonancia fr de los arrollamientos y verificar que este valor esté lejos de la frecuencia de la componente transitoria de las fuerzas de cortocircuito (50 ó 60 Hz) como de la componente permanente (100 ó 120 Hz).
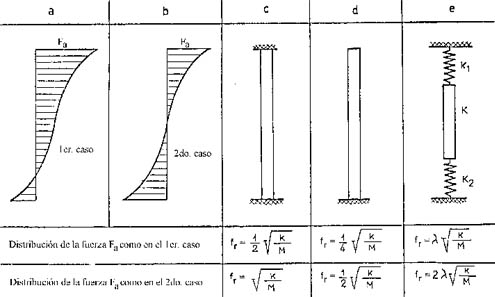
Para simplificar la determinación de fr el modelo del arrollamiento de la figura 773 se puede substituir con un sistema continuo, es decir el arrollamiento se considera como una barra que vibra longitudinalmente.
Son aplicables las siguientes expresiones:
-
a) Las dos extremidades fijas o libres figura 806 (c)
-
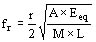
b) Una extremidad fija y la otra libre figura 806 (d)
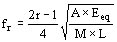
siendo:
A: superficie del disco ocupada por los distanciadores (cm2)
Eeq: módulo de elasticidad equivalente del arrollamiento (kg/cm2)
M: masa del arrollamiento (kg seg2/cm)
L: altura del arrollamiento
r: orden de la armónica (r = 1,2,3,..)
La determinación del valor de Eeq se debe realizar teniendo en cuenta que la característica del devanado debido a su aislamiento no es lineal y además que la carga aplicada es de carácter dinámico.
El problema de evaluar el módulo de elasticidad dinámico resulta difícil.
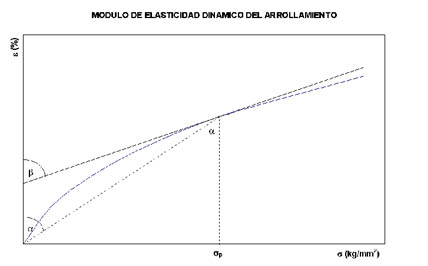
Para determinar su valor se puede utilizar un método relativamente simple (no riguroso) que consiste en calcular la derivada de la curva estática e = f(s ) del arrollamiento, en el punto correspondiente a la precompresión s p.
En la figura 807 se observa que el valor dinámico es proporcional a tg b y que por lo tanto resulta más grande del valor estático que es proporcional a tg a.
Evidentemente la más importante es la frecuencia fundamental y por lo tanto los cálculos se realizan para r = 1 (fundamental).
La presencia de armónicas y su amplitud depende del tipo de deformación dinámica que se aplica inicialmente a la barra, es decir antes de dejarla vibrar libremente.
Normalmente las armónicas disminuyen rápidamente a medida que aumenta r y en muchos casos se pueden despreciar.
Para aplicar las fórmulas indicadas a los arrollamientos se debe considerar la distribución de las fuerzas axiales a lo largo de la altura del devanado.
Se pueden considerar dos casos principales: que la distribución sea asimétrica respecto al eje de simetría del arrollamiento o bien que sea simétrica.
En el primer caso figura 806 (a) la mayor parte del arrollamiento está sometido a una fuerza directa en el mismo sentido. Las vibraciones a lo largo del devanado están en fase y las fórmulas se pueden aplicar directamente.
En el segundo caso figura 806 (b) mitad del arrollamiento está sometido a una fuerza en un sentido y la otra mitad en sentido contrario. Las vibraciones de las dos mitades están desfasadas en 180° , es decir cada mitad vibra por cuenta propia.
En las fórmulas tanto la altura como la masa del arrollamiento se adoptan igual a la mitad y la frecuencia de resonancia resulta dos veces mayor que para el caso anterior.
Si se tiene en cuenta el efecto del aislamiento en los extremos de los arrollamientos se debe examinar el sistema indicado en la figura 806 (e), que consiste en una barra que representa el arrollamiento y dos resortes que representan el aislamiento de ambos extremos.
Las respectivas constantes elásticas (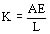
) son K, K1 y K2.
La frecuencia de resonancia en este caso resulta:
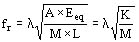
el valor de l se obtiene encontrando la solución de la ecuación trascendental:
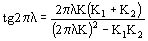
su resolución resulta más fácil por métodos gráficos.
En las construcciones normales frecuentemente se puede suponer que las superficies ocupadas por los distanciadores de los arrollamientos son iguales (A1 = A2 = A), que las alturas de los arrollamientos son iguales (L1 = L2) y que los módulos de elasticidad de los aislantes de ambos extremos son iguales (E1 = E2).
En consecuencia l resulta solamente función de E1/Eeq.
La frecuencia de resonancia baja con la presencia de aislamiento en los extremos de los devanados (valor bajo de la relación E1/Eeq) debido a que el valor de l resulta pequeño.
En el caso límite que la relación E1/Eeq tiende a un valor muy grande l tiende a 0,5 que es el valor que corresponde para el caso de una viga empotrada rígidamente en ambos extremos como indicado en la figura 806(c).
Conclusiones
Por lo expuesto anteriormente se concluye que para evaluar la capacidad de los devanados para resistir las fuerzas de cortocircuito es necesario conocer las siguientes magnitudes referidas a cada uno de los arrollamientos.
- Corriente de cortocircuito, número de espiras y número de conductores en paralelo
- Masa y dimensiones geométricas
- Distancias de los devanado a los yugos
- Cantidad, dimensiones y aislamiento de los conductores de cada disco
- Cantidad y dimensiones de los separadores radiales y distanciadores axiales
- Límite de fluencia convencional y módulo de elasticidad del material de los conductores (s 0.2, E)
- Módulos de elasticidad estáticos y dinámicos de los materiales aislantes (E1, E2, Eeq)
- Valor de la precompresión (presión de sujeción)
De estas magnitudes aquellas eléctricas y dimensionales se pueden conocer con suficiente precisión. Las otras dependen de algunos factores no siempre bien controlados. En particular el límite de fluencia s 0.2 depende de como el material de los conductores ha sido endurecido durante su elaboración.
Los módulos de elasticidad de los materiales aislantes dependen de los ciclos de estabilización experimentados por el arrollamiento y de la presión de trabajo.
Esta última depende en sentido radial de como son tensados los conductores durante la construcción del arrollamiento, de las tolerancias para el montaje de los listones, de los apartamiento durante el proceso de secado etc., y en sentido axial de la presión de fijación aplicada y de como ésta se mantiene en el tiempo.
Se puede concluir que para garantizar la capacidad del transformador a soportar los esfuerzos electrodinámicos, no es suficiente con la verificación por cálculo y que las características de los materiales sean las requeridas, es imprescindible una adecuada tecnología de producción y rigurosos controles de calidad durante el montaje.
El estudio de los métodos a utilizar para estos controles es tema de interés tanto para los constructores como para quienes utilizan las máquinas.
Bibliografía
- M. WATERS "The short circuit strength of power transformers" Macdonal & Co Publishers Ltd. - London 1966.
- H. P. MOSER y otros "Transformerboard" Special print of Scientia Electrica - Vermont, U.S.A. 1979.
- FILIPPO COPPADORO "Comportamento dei trasformatori in caso di corto circuito" Elettrificazione, noviembre 1967.
- BERTAGNOLLI, CAPRIO, DE MARTIN "La tenuta al corto circuito" I trasformatori di grande potenza
- Civitavecchia (RM), noviembre 1992.
- B. SOLLERGREN "Calculation of short-circuit forces in transformers" - Working Group 12-04 of Study Committee Nº 12 - Revista ELECTRA Nº 67.
- KIYOTO HIRAISHI, YASURO HORI, SHIGERU SHIDA "Mechanical Strength of Transformer Windings under Short Circuit Conditions" - IEEE Transactions PAS Nº 5 - 1971.
- MUKUND R. PATEL " Dynamic Response of Power Transformers under Axial Short Circuit Forces" Part. I and II - IEEE Transactions PAS Nº 5 - 1973.
- G.P. SCENDRATE - G.L. SIGAUDI "Analysis of leakage flux distribution and related parameters with reference to different design solutions" I.E.L Legnano Italia.
- R. BOERSMA, J. WILDEBOER "Résistance mécanique des enroulements internes des transformateurs aux forces radiales en cas de courtcircuit" Rap. 147 CIGRE 1962.
- Antonio AZZIZ - Alvaro PORTILLO "Cálculo de las fuerzas de cortocircuito en transformadores.
Copyright 2008 - 2012 INDUCOR INGENIERIA S.A. | Todos los derechos reservados | CCS | HTML