CALCULO Y DISEÑO DE MAQUINAS ELECTRICAS
APENDICE 19 - REACTANCIAS Y CONSTANTES DE TIEMPO DE LAS MAQUINAS SINCRONICAS
Introducción
En el cálculo de las máquinas eléctricas los temas de reactancias funcionales de régimen permanente están resueltos en la bibliografía clásica con varias modalidades, obteniéndose resultados razonablemente acertados.
Es más, frecuentemente hay máquinas sincrónicas con una jaula amortiguadora, intuitivamente esta máquina fuera de sincronismo tiene un comportamiento que puede asimilarse al de un motor asincrónico.
Se observan muchos temas, de los que surgen muchas preguntas que merecen respuesta.
Buscando respuestas en la bibliografía, en varias ocasiones nos hemos topado con respuestas que orientan pero no ayudan al cálculo de los parámetros de interés.
Finalmente un artículo de 1958 nos resolvió el problema en detalle, y nos permitió profundizar aún más los temas que siguen.
Resultados de interés
Quien estudia el funcionamiento de las máquinas sincrónicas en regímenes cualesquiera identifica:
Reactancia sincrónica
Reactancia transitoria
Reactancia subtransitoria
También se trata de determinar constantes de tiempo
Constante de tiempo transitoria
Constante de tiempo subtransitoria
El interés en identificar estos valores, señala caminos experimentales, que pueden serrecorridos con independencia del conocimiento de la intimidad de la máquina.
El profundizar estos temas muestra que en general los parámetros tienen distinto valores según se los identifique sobre el eje directo o en cuadratura (transversal).
Deseamos ahora observar estos temas desde el punto de vista del constructor veamos el artículo bibliográfico.
"Calcul des réactances, résistences et constantes de temps des machines syncrhones"
por: René DAGUET
(Traducido por Ing. Jorge N. L. Sacchi y Ing. Alfredo Rifaldi marzo 1998)
Cálculo de las reactancias, resistencias y constantes de tiempo de las máquinas sincrónicas
Generalidades
Definiciones
Las reactancias, resistencias y constantes de tiempo de máquinas sincrónicas constituyen elementos esenciales que permiten estudiar los diferentes regímenes de funcionamiento de las máquinas.
Es así que gracias a su conocimiento, se pueden determinar las condiciones de funcionamiento no sólo en régimen permanente, sino aún bajo fenómenos accidentales rápidos como: cortocircuito brusco, desconexión de la red, perdida la excitación, etc. Asimismo nos proponemos estudiar las condiciones de funcionamiento en paralelo (ver D 520), evaluar las corrientes de falla y estudiar los regímenes desequilibrados.
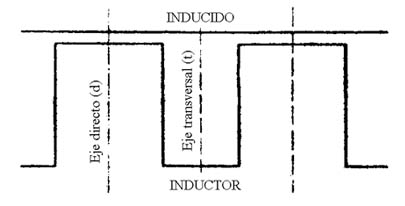
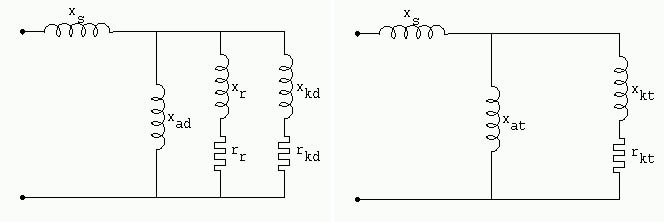
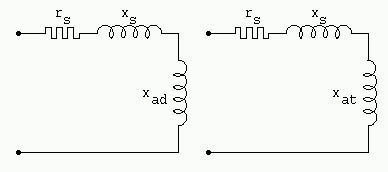
Tiene lugar considerar dos categorías de reactancias: las reactancias que se observan según el eje directo (figura 1088 - Reactancias según el eje directo) y aquellas que se observan según el eje transversal (dicho igualmente en cuadratura) (figura 1089 - Reactancias según el eje transversal). Nosotros distinguiremos dos familias de reactancias con la ayuda de los índices d (directo) y t (transversal) (figura 1090 - Reactancias de las máquinas sincrónicas).
Según el eje directo nosotros encontramos (figura 1088 - Reactancias según el eje directo) xs reactancia de fuga de inducido; y además el paralelo de:
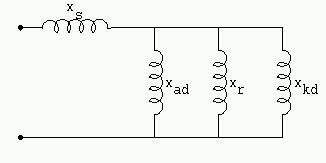
xad reactancia de entrehierro
xr reactancia de fuga de inductores
xkd reactancia del circuito amortiguador
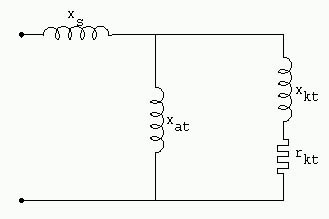
Según el eje transversal ahora no encontramos más el arrollamiento inductor, sólo encontramos (figura 1089 - Reactancias según el eje transversal):
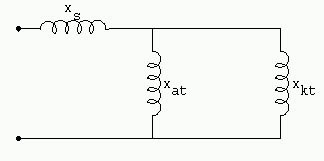
xs reactancia de fuga del inducido
xat reactancia de entrehierro
xkt reactancia del circuito amortiguador
Reactancias sincrónicas
En régimen permanente, sólo las reactancias xs y xad deben considerarse según el eje directo ellas están en serie su suma define una reactancia llamada sincrónica xd:
Xd = Xs + Xad
Por analogía según el eje transversal se podrá definir xt reactancia sincrónica transversal, que es:
Xt = Xs + Xat
(ver D 482 páginas 16, 17 y 18)
Regímenes accidentales
El régimen accidental más frecuente es el cortocircuito en bornes en la proximidad de la máquina, de manera que se pueda considerar la impedancia de carga (externa) sobre la cual entrega esta máquina como prácticamente nula.
Recordemos que en todo circuito eléctrico cerrado de resistencia óhmica nula o despreciable, el número de líneas de fuerza que circulan entre inducido e inductor tiende a mantenerse constante. Si e es la fuerza electromotriz de inducido, r su resistencia y L su inductancia se tiene:
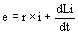
Si se cierra el circuito inducido bruscamente sobre una resistencia exterior nula se tiene
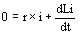
y considerando despreciable rresulta
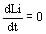
de donde Li = cte
Como L=F /i por definición, F es el flujo que atraviesa el inducido, e i es la corriente se tiene
F = Li = cte
Diciendo esto en otra forma, al momento del cortocircuito el flujo bruscamente cesa de variar; su eje queda fijo, no gira más junto con los inductores, e induce en estos últimos, como también en el circuito amortiguador si existe, corrientes que son determinadas y se refieren a los diagramas equivalentes de las figuras 1091 y figura 1092 (Diagramas equivalentes de cortocircuito) con la ayuda de impedancias xr y xkd en el eje directo y xkt en el eje transversal; estas corrientes decrecen siguiendo una ley exponencial dependiente de las constantes de tiempo de los circuitos considerados, las que están condicionadas por las resistencias rr, rkd y rkt.
Funcionamientos monofásicos
Se sabe, del teorema de Leblanc, que en el caso de funcionamiento monofásico, el campo que es fijo, puede ser considerado como suma geométrica de dos campos rotantes en sentidos inversos, de amplitudes mitad del campo fijo, una sobre el eje que gira en sincronismo con el inductor la otra en sentido inverso, atravesando continuamente los circuitos de inductor (arrollamientos de excitación y amortiguadores). Nosotros volveremos más adelante sobre este funcionamiento, pero, desde ahora reconocemos que el campo que gira en sentido inverso que el de la máquina provoca la aparición en el inducido de una reactancia suplementaria llamada reactancia inversa y que designaremos xi.
Reactancia homopolar x0
Cuando el arrollamiento inducido posee un borne neutro se puede definir la reactancia homopolar x0 que es igual al cociente del término fundamental de una componente homopolar de tensión aplicada entre las fases y el punto neutro por el término fundamental de corriente homopolar que ella determina (i0).
La reactancia homopolar está muy influenciada por el acortamiento del paso del devanado. Para un acortamiento a = 0.666 las corrientes que circulan en las dos secciones de conductor que implica la ranura son iguales en fase pero en oposición. Se concluye que las fugas en las ranuras en esas condiciones resultan muy pequeñas.
El conocimiento de esta reactancia homopolar es útil en particular para la determinación de las protecciones que se basan sobre el valor de la corriente de falla que circula hacia el neutro.
Influencia del estado de saturación de la máquina
La reactancia opuesta por una máquina a una variación de la tensión en bornes es función del estado de saturación de su circuito magnético que puede variar, pero sobre todo en el curso del fenómeno estudiado si la variación de tensión es importante.
Salvo convención en contra, las reactancias de una máquina se suponen referidas al estado no saturado. Este es el caso donde las reactancias axiales y transversales de la máquina son independientes.
Reactancias transitorias y subtransitorias axiales
Sin embargo se deroga esta regla general para definir la reactancia subtransitoria axial x''d y la reactancia transitoria axial x'd las cuales se emplean frecuente en la determinación de las corrientes de cortocircuito bajo tensión normal.
La reactancia transitoria x'd es igual al cociente de la tensión nominal por el valor inicial de la componente simétrica de la corriente de cortocircuito brusca bajo esa tensión, valor de corriente disminuido en el término del decremento muy rápido subtransitorio y vectorialmente de la corriente preexistente.
La reactancia subtransitoria x''d es igual al cociente de la tensión nominal por el valor inicial de la componente simétrica de la corriente de cortocircuito brusco bajo esta tensión, deducción hecha vectorialmente de la corriente preexistente. La máquina está inicialmente en vacío o en régimen nominal, siguiendo una convención definida en cada caso.
La saturación del circuito magnético puede entonces ser apreciada y tiene lugar aplicar un factor de corrección (ver D 480).
Máquinas sincrónicas fuera de sincronismo
El funcionamiento fuera de sincronismo puede ser debido a un mal acoplamiento (paralelo), una sobrecarga, una baja tensión (o de las dos causas últimas simultáneas) provocando una desconexión. En el funcionamiento fuera de sincronismo, dos casos pueden ser observados:
El circuito de los inductores queda cerrado
El circuito de los inductores está abierto
Se puede igualmente hacer funcionar momentáneamente una máquina sincrónica en régimen asincrónico, cuando por ejemplo se desea arrancar sobre una jaula amortiguadora un motor sincrónico o un compensador sincrónico o asimismo si se quiere usar un alternador, por este procedimiento, y próximo al sincronismo se efectúa la sincronización al final del arranque (ver D 510 pág. 5).
Circuito inductor cerrado
En el caso más frecuente el circuito de inductor queda cerrado, se tiene el diagrama equivalente de la figura 1093 (Diagrama equivalente, fuera de sincronismo, con el circuito inductor cerrado) y es usado para buscar para distintos resbalamientos el valor de la reactancia total.
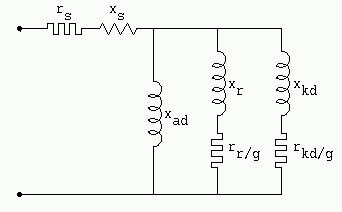
Las resistencias se hacen muy importantes con deslizamientos pequeños porque se debe dividir su valor por el deslizamiento, entonces aquellas pueden ser despreciadas cuando se presenta un cortocircuito instantáneo, como en ese momento el deslizamiento a continuación de la inmovilización brusca del flujo de estator, es próximo a 1.
Para obtener la impedancia total, sumaremos a la impedancia estatórica definida porrs y xs las tres impedancias en paralelo xad 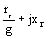 ;
; 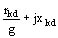 ;
;
Como estas impedancias están en paralelo nosotros pasamos por intermedio de las admitancias, para las cuales los términos reales e imaginarios se suman aritméticamente. Nosotros tenemos:
admitancia de entrehierro
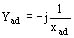
admitancia de la jaula
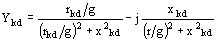
admitancia de los inductores
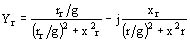
La suma de estas tres admitancias Yrd se obtiene de la forma:
Yrd = Yad + Ykd + Yr = a - j b
donde:
a suma de partes reales de Yad , Ykd, Yr
b suma de partes imaginarias de las mismas cantidades.
Retornando a las impedancias tenemos:
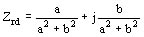
Sumando Zs a Zrd obtenemos la impedancia total de la máquina que será de la forma Zd = c + jd donde la magnitud del módulo será
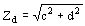
Se deducirá la corriente absorbida por el estator is = 1 / Zd
y el par correspondiente al deslizamiento g considerado
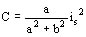
Aplicación numérica
Tenemos una máquina de 570 kW 3000 V corriente nominal 110 A, la reactancia de referencia de la máquina es igual a:
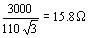
Nosotros vamos a ver luego de los cálculos los diferentes parámetros en valor unitario. Por ejemplo, la reactancia por fase estatórica que es 2.65 W será en valor unitario
xs = 2.65 / 15.8 = 0.168.
Nosotros hemos por ahora calculado
rs = 0.0314
xad = 0.865
rkd = 0.137
xkd = 0.23
xr = 0.268
rr = 0.0418
Calcularemos el punto correspondiente a un resbalamiento de
g = 0.4
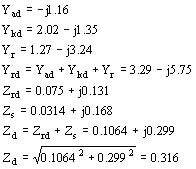
corriente absorbida por el estator:
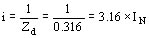
El par en valor unitario ahora tiene el valor
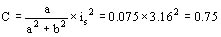
El par en valor unitario referido al par nominal será entonces:
C´ = 0.75 x Cn
donde CN está dado en kgm nosotros obtenemos naturalmente C' en kgm.
Se puede rehacer este cálculo según el eje transversal a fin de verificar que la corriente absorbida, y el par obtenido son diferentes de aquellos calculados según el eje directo.
Circuito de inductor abierto
En este caso el inductor se comporta exactamente como el rotor de jaula de un motor asincrónico.
Si un alternador se desconecta y si las protecciones interrumpen el inductor, nosotros nos encontraremos en el caso del circuito equivalente (figura 1094 - Diagrama equivalente fuera de sincronismo, con el circuito inductor abierto).
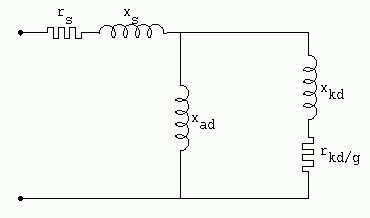
El deslizamiento se encuentra entonces muy próximo a 0 al inicio del fenómeno, pues aumenta con la disminución de velocidad de la máquina y se puede tratar el problema como para el circuito de inductor cerrado haciendo simplemente abstracción de la rama rr xr.
Desde que se rompe el sincronismo se ve que el eje del inductor se desplaza en relación al eje del flujo estatórico y se debe, para serriguroso, considerar los diagramas equivalentes sucesivamente según el eje directo y según el eje transversal. Si las impedancias resultantes correspondientes a estas dos posiciones son sensiblemente diferentes, constataremos una pulsación en la corriente que atraviesa la máquina en los dos casos arriba vistos.
Cálculos de las reactancias
Reactancias trifásicas
En la exposición completa nosotros trataremos siempre las impedancias referidas a una fase del sistema trifásico y evaluaremos sus valores unitarios. Nosotros recordamos que por convención, se denomina reactancia de referencia (base) de una máquina sincrónica el valor determinado por el cociente de la tensión por fase y la corriente nominal de la máquina: por ejemplo para una máquina trifásica la reactancia base es Zapp = U / I Ö 3, siendo U la tensión en bornes de la máquina U / Ö 3 expresa la tensión de fase, y Zapp está expresada en ohm por fase.
Si por otra parte, nosotros hemos calculado cierta reactancia de la máquina xs por ejemplo (reactancia expresada ella también en ohm por fase) el valor unitario xs estará dado por el cociente xs / Zapp.
Características del alternador estudiado en los ejemplos numéricos
Para facilitar la comprensión de las distintas fórmulas nosotros hemos dado a título de ejemplo numérico, el cálculo de las reactancias de un alternador que tiene las siguientes características:
Potencia - 70 MVA
Tensión nominal - 15 kV
Corriente nominal - 2700 A
Frecuencia - 50 Hz
Amper vueltas de entrehierro ATd - 15700
Reacción de inducido R - 9250
Diámetro D - 710 cm
Longitud del paquete de hierro estatórico La - 210 cm
Conductores en serie por fase N2 - 128
Número total de ranuras Ns - 384
Paso del arrollamiento a - 5/6
Número total de barras amortiguadores Nb - 320
Factor de arrollamiento debido al número de ranuras por polo y por fase K1 - 0,955
Factor de arrollamiento debido al acortamiento del paso K2 - 0.9667
Número de polos P - 40
Ancho de la ranura de estator d - 2.35 cm
Altura total ocupada por los conductores h4 - 12.26 cm
Altura del istmo h5 - 1.46 cm
(Para estas tres últimas características ver figura 11 en D 480 - 7)
Reactancia base Zapp - 15000 / 2700 Ö 3 = 3.21 W
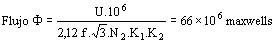
Reactancia de fuga de inducido xs
La determinación del flujo de fuga del arrollamiento inducido comprende el cálculo del flujo de fuga de las ranuras y del flujo de fuga de las conexiones (ver D 480 - 14)
Se puede igualmente utilizar la fórmula de Alger que es la siguiente:
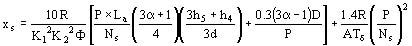
El primer término entre corchetes es relativo a las fugas debidas a las ranuras, el segundo a las fugas debidas a los desarrollos (cabezas de bobinas).
El término
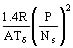
expresa las fugas en zigzag.
Ejemplo: xs = 0.0964
Reactancias de entrehierro según el eje directo (o longitudinal) xad
Está dada por la fórmula:
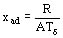
Ejemplo: xad = 0.59
Reactancia de entrehierro según el eje transversal xat
Esto se puede obtener con la ayuda de un trazado de campo magnético según el eje transversal (método de Lehman D 420) de lo que se extrae el término fundamental.
Este método es laborioso, esto es debido a que se establecen las curvas que resumen este modo de cálculo en función de diferentes parámetros del alternador (entrehierro máximo, mínimo, paso polar, arco polar, etc.).
Se puede así evaluarrápidamente xat con la ayuda de la fórmula siguiente:
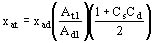
Ejemplo numérico
Para la máquina que nos sirve de ejemplo se tiene:
entrehierro mínimo 21.5 mm
paso polar 558 mm
arco polar 365 mm
entrehierro máximo 30 mm
número de canales de ventilación 35
ancho del diente 34.5 mm
Nosotros calcularemos ahora las siguientes relaciones:
entrehierro mínimo/paso polar = 0.036
arco polar/paso polar = 0.665
entrehierro máximo/entrehierro mínimo = 1.4
longitud total/número de canales + 1 = 2100/36 = 58.5
ancho ranura/ancho diente = 0.68
ancho ranura/entrehierro mínimo = 1.09
At1 y Ad1 están dados por las curvas de las figuras 1110A, figuras 1110B y figuras 1110C (Curvas para calcular la reactancia de entrehierro según el eje directo Fundamental Ad1) y figuras 1111A, figuras 1111B y figuras 1111C (Curvas para calcular la reactancia de entrehierro según el eje transversal Fundamental At1).

Cs es un coeficiente que tiene en cuenta el ancho de los dientes, de las ranuras y del entrehierro mínimo. Esta dado por la curva de la figuras 1112 (Curvas para calular la reactancia de entrehierro según el eje transversal Coeficiente Cs).
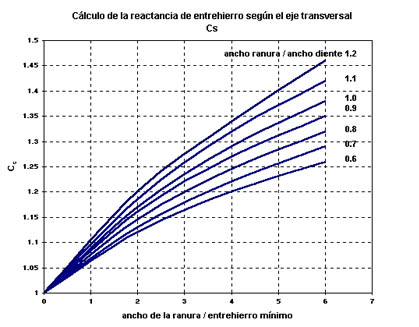
Cd es el coeficiente de influencia de los canales de ventilación estatóricos. El está dado por la curva de la figuras 1113 (Curvas para calcular la reactancia de entrehierro según el eje transversal Coficiente Cd).
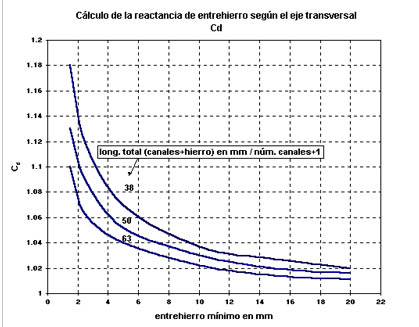
Se encuentra:
At1 = 0.35 ´ 1.37 = 0.48
Ad1 = 1.08 ´ 0.82 = 0.885
Cs = 1.075
Cd = 1.01
xat = 0.344
Reactancia sincrónica según el eje directo xd
Refiriéndola al diagrama equivalente del alternador en régimen permanente se ve que:
xd = xs + xad
Ejemplo: xd = 0.09648 + 0.59 = 0.68648
Reactancia sincrónica según el eje transversal xt
xt = xs + xat
Ejemplo: xt = 0.09648 + 0.334 = 0.43048
Reactancia debida al flujo de fugas de los inductores xr
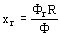
F r es el flujo de fuga de los inductores. Este flujo se obtiene por un trazado de Lehman dando el número de tubos de permeancia unitaria que se escapan lateralmente de un polo a otro. Sea n este número de tubos por unidad de longitud (ver D 420), l la longitud afectada por las fugas. Se toma ordinariamente
l = La + t/2
t es el paso polar
Se tiene finalmente:
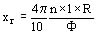
donde l en cm R en AT, F en maxwells.
Ejemplo:
n = 3.2
l = 237.9
0.4p .n.l. = 960
xr = 0.134
Reactancia de los amortiguadores según el eje directo
ella está dada por la fórmula
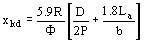
b es el número de barras amortiguadores por polo.
Ejemplo:
b = 8
xkd = 0.0465
Reactancia de amortiguadores según el eje transversal
se toma:
xkt = 0.75 xkd
Ejemplo: xkt = 0.0348
Reactancia transitoria según el eje directo x'd
En el momento del fenómeno transitorio, el subtransitorio ya pasó, la reactancia de fuga de los inductores xr se encuentra, sobre el diagrama equivalente en paralelo con xad
Nosotros tenemos:
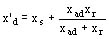
Ejemplo: x'd 0.2058
Reactancia transitoria según el eje transversal x't
Siguiendo este eje la reactancia xr no aparece, en consecuencia x't = xt
Reactancia subtransitoria según el eje directo x''d
En el momento del fenómeno subtransitorio la reactancia xr está en paralelo con xad y xkd reactancia de los amortiguadores según el eje directo, nosotros tenemos:
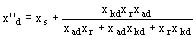
Ejemplo:
xs = 0.0965
xkd = 0.0465
xad = 0.59
xr = 0.137
x''d = 0.1294
Reactancia subtransitoria según el eje transversal x''t
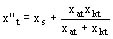
Ejemplo: x''t = 0.1278
Reactancia homopolar x0
Se puede emplear la fórmula siguiente debida a Alger (ver bibliografía)
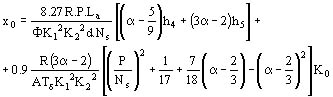
El factor K0 es para considerar cuando la máquina está munida de amortiguadores. Se toma igual a 0,5 como en el ejemplo aquí arriba
Ejemplo: x0 = 0.0645
Reactancia inversa xi es la media entre x''d y x''t
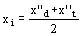
Ejemplo:
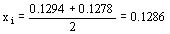
Reactancias monofásicas
Se evalúan partiendo de las reactancias calculadas precedentemente en caso de funcionamiento trifásico. Se debe introducir en las fórmulas el valor de la reacción de inducido trifásica. En el caso del monofásico, con dos terceras partes de ranuras bobinadas (monofásicas de línea a línea), la reacción de inducido para una máquina determinada es Ö 3 veces más pequeña que la trifásica (ver D 480).
Se tiene en efecto
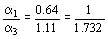
Para el monofásico no se utiliza más que una rama del trifásico, o sea 1/3 de las ranuras (entre línea y punto neutro), la reacción de inducido es 3 veces más pequeña que la trifásica. La reactancia de fugas estatórica será entonces en monofásico, de línea a línea.
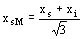
y para monofásico entre línea y punto neutro
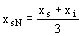
A partir del funcionamiento trifásico, se puede llegar cuando una fase está cortada, al funcionamiento monofásico denominado de línea a línea. Cuando el alternador funciona sobre una sola rama, se emplea la expresión entre línea y punto neutro.
Monofásico línea a línea según el eje directo
Reactancia sincrónica:
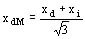
Ejemplo: xdM = 0.47
Reactancia sincrónica transitoria:
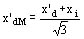
Ejemplo: x'dM = 0.194
Reactancia subtransitoria sincrónica:
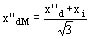
Ejemplo: x''dM = 0.149
Monofásico entre línea y punto neutro según el eje directo
Reactancia sincrónica:
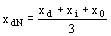
Ejemplo: xdN = 0.293
Reactancia sincrónica transitoria:
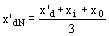
Ejemplo: x'dN = 0.133
Reactancia sincrónica, monofásica subtransitoria:
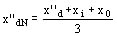
Ejemplo: x''dN = 0.1075
Monofásica entre línea y punto neutro según el eje transversal
Para estas reactancia es suficiente en las expresiones precedentes reemplazarrespectivamente xd, x'd, x''d por xt, x't, x''t
Cálculo de las resistencias
Resistencia de inducido rs
rs = pérdidas Jole del estator + pérdidas suplementarias / kVA nominales
Pérdidas suplementarias ver artículo alternadores en D 482 - 7
Ejemplo:
pérdidas por efecto Joule = 220 kW
pérdidas suplementarias = 120 kW
potencia nominal = 70000 kVA
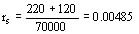
Resistencia de los inductores rr
La resistencia en ohms rr se transforma en valor unitario
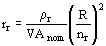
Ejemplo:
R = 9250
nr = 21.5
VAnom = 70000 ´ 103 VA
rr = 0.187 W
rr = 0.0005
R = amper vueltas de reacción de inducido
nr = número de espiras por un polo del inductor
Resistencia de los amortiguadores según el eje directo
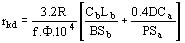
Cb coeficiente que tiene en cuenta la resistividad de las barras (tomar 1 para el cobre, 4 para el latón)
Ca coeficiente que tiene en cuenta la resistividad del anillo amortiguador (tomar 1 para el cobre, 4 para el latón)
D diámetro en cm
P número de polos
Lb longitud de las barras en cm
Sb sección de las barras en cm2
Sa sección del anillo en cm2
f flujo en megamaxwels
B número de barras
Ejemplo:
D = 710 mm Sb = 2.25 cm2 Ca = Cb = 1
P = 40 cm Sa = 8 cm2
Lb = 210 cm F = 66 M Maxwells B = 8
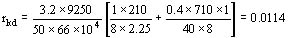
Resistencia del amortiguador según el eje transversal
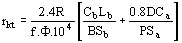
Ejemplo:
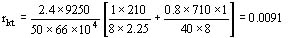
Nota: las constantes 2,4 y 0,8 se hacen respectivamente 7,3 y 0,2 para los amortiguadores sin ligazón de polo a polo.
Cálculo de las constantes de tiempo
Definición
La constante de tiempo de un circuito determinado de una máquina sincrónica se obtiene dividiendo la reactancia del circuito (lo que incluye su propia reactancia, y la de los circuitos derivados que figuran en el diagrama equivalente) por el producto 2p veces la frecuencia por la resistencia del circuito considerado.
Constante de tiempo de inducido bajo cortocircuito brusco (las inductancias están cerradas) ts: en este momento, el flujo de inducido está inmovilizado (los polos de inducido formados por los sucesivos dientes polarizados, están momentáneamente fijos) como los polos inductores continúan su rotación; la reactancia que interviene es la llamada reactancia inversa xi; así la situación relativa inductor - inducido es la misma que cuando los polos están fijos y acompañados por el campo rotante estatórico.
La resistencia de inducido se designa con rs y se tiene
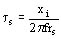
Para el alternador según el ejemplo se obtiene:
rs = 0.00485 p.u. ts = 0.0845 s
Constante de tiempo subtransitoria t''d
Es la constante de tiempo de los amortiguadores, el alternador ha sido puesto en cortocircuito. La reactancia vista es la de los amortiguadores xkd con en paralelo xad, xr y xs figura 1137 - Constante de tiempo subtransitoria, alternador en cortocircuito)
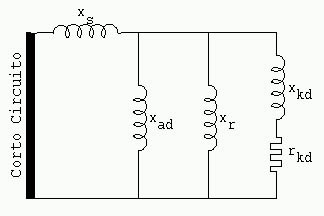
La resistencia que interviene es la de los amortiguadores rkd
Se tiene entonces:
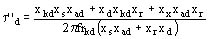
recordando que xd = xs + xad
Ejemplo: rkd = 0.0114 t''d = 0.0275 s
Constante de tiempo transitoria t 'd
Esta es la constante de tiempo de los inductores, el inducido está puesto en cortocircuito. Esta constante caracteriza el fenómeno de cortocircuito una vez desaparecido el período subtransitorio, es decir cuando la corriente que atraviesa los amortiguadores ha desaparecido (esto se traduce, por la desaparición de xkd, en el diagrama equivalente de la figura 1138 Constante de tiempo transitoria, inducido en cortocircuito).
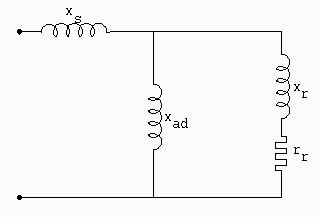
La resistencia a considerarrr es la resistencia de los inductores
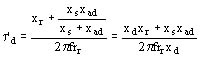
Ejemplo: rr = 0.0005 t'd = 1.38 s
Constante de tiempo de los inductores el alternador se encuentra en vacío t'd0
El diagrama equivalente está dado por la figura 1138 (Constante de tiempo del inductor, alternador en vacío)
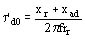
y se puede también escribir
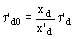
Ejemplo: t'd0 = 4.6 s
Constante de tiempo de inducido (inductor abierto) t0s
El alternador separado de la red, con su excitación cortada generalmente por las protecciones. t 0s es la constante de tiempo que condiciona la desaparición de la tensión de inducido. El alternador, no está más en sincronismo, pasa sucesivamente de la posición directa a la posición transversal y la reactancia que entra en juego es una media entre xd y xt.
Los diagramas equivalentes están dados por las figuras 1139AB (Constante de tiempo de inducido, inductor abierto)
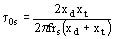
Ejemplo: t0s = 0.346 s
Constante de tiempo según el eje transversal de amortiguador, el inducido está puesto en cortocircuito (t''t)
El diagrama equivalente está dado por la figura 1140 (Constante de tiempo según el eje transversal del amortiguador, inducido en cortocircuito)
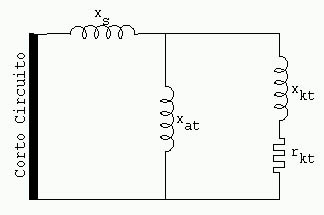
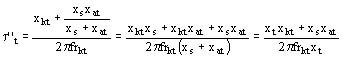
Ejemplo: t''t = 0.0385 s
Constante de tiempo según el eje transversal del arrollamiento amortiguador (estando el inducido en circuito abierto)
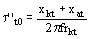
ver figura 1141 (Constante de tiempo según el eje transversal del amortiguador, inucido abierto)
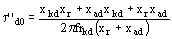
Ejemplo: t ''t0 = 0.129 s
Constante de tiempo según el eje directo del arrollamiento amortiguador (el inducido se encuentra en circuito abierto) t ''d0
Con lo que muestra el diagrama equivalente (figura 1142 - Constante de tiempo según el eje directo del amortiguador, inducido abierto) se encuentra t ''d0
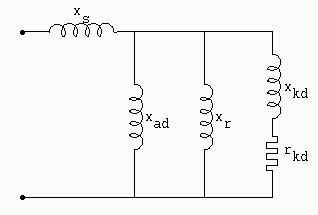
Ejemplo: t ''d0 = 0.0437 s
Nota: si comparamos las expresiones de t ''d0 y de t ''d nosotros vemos en todos los cálculos hechos que 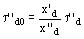
Asimismo si nosotros comparamos t ''t0 y t ''t nosotros vemos que
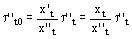
puesto que x't = xt
Medición de reactancias
Para xad, xd, xat, xs ver D 482
Reactancia sincrónica transversal
Un primer método se indica en D 482 - 17 otro método consiste en impulsar la máquina como motor sincrónico sin carga en su eje y con una tensión constante aplicada a sus bornes. La tensión de excitación se reduce progresivamente a cero después se aumenta en sentido negativo, provocando así, después del momento en que la tensión es nula, un aumento de la corriente de inducido.
Aumentando progresivamente y gradualmente la corriente de excitación negativa, se puede encontrar la corriente máxima Imax que permite aún la estabilidad y correspondiente a la excitación máxima negativa estable.
Entonces el eje de los polos inductores se encuentra coincidente con el eje transversal. Donde
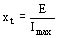
E tensión aplicada expresada en valor unitario
Imax corriente estatórica máxima, en valor unitario
para la excitación negativa máxima que asegura todavía la estabilidad (véase fig. 28 en D 510 - 12) sobre esta figura se ve que la corriente de inducido DB correspondiente al límite de estabilidad permite obtener xt = U / DB
Si U y DB se expresan en valores unitarios se obtendrá igualmente xt en valor unitario.
Es preferible hacer este ensayo a tensión reducida a fin de disminuir todavía las pérdidas que entonces son muy pequeñas.
Reactancia transitoria según el eje directo x'd
Esta reactancia se deduce de un ensayo en cortocircuito brusco efectuado en vacío a la velocidad normal. Se extrapola el valor de corriente hasta el instante t = 0 de aplicación brusca y se desprecian las primeras alternancias influenciadas por el subtransitorio (véase fig. 80 en D 482 - 19 se aclara que t''d es la abscisa de E).
Reactancia subtransitoria según el eje directo X''d y según el eje transversal
1er. método - referirse a D 482 - 17
Al ejecutar el primer método se notará que, en este ensayo, las corrientes rotóricas están a la frecuencia de sincronismo en lugar de tener un decremento aperiódico relativamente lento, como en un ensayo de cortocircuito brusco que es la base de la definición de las reactancias subtransitorias.
Esto resulta, sobre todo cuando los polos implican piezas macizas, una repartición diferente de las corrientes en la profundidad del metal, que puede por tanto afectar, en una proporción no despreciable, los valores observados de reactancias.
El empleo del método no es entonces recomendable en el caso de máquinas de polos macizos y particularmente en los turboalternadores; se admitirá, para estos últimos, que la reactancia subtransitoria transversal es igual a la reactancia subtransitoria axial deducida del ensayo en cortocircuito brusco con el método de la tensión de restablecimiento.v
Para las máquinas de polos salientes se tendrá en cuenta la influencia de la saturación multiplicando los valores deducidos del ensayo, a la parada por los mismos coeficientes correctivos que en el caso de la medición por puesta en cortocircuito brusco.
2do. método
Otro método, que puede ser empleado cuando se está seguro que, bajo cortocircuito brusco las tres fases se ponen en cortocircuito al mismo tiempo, o al menos con una diferencia que no pase de 10 grados eléctricos, y el está basado sobre la componente asimétrica máxima representada por la línea media (figura 1143 - Medida de la reactancia subtransitoria. Oscilograma tomado en cortocircuito en una de las fases compuestas) sobre el oscilograma tomado en cortocircuito sobre una de las fases componentes.
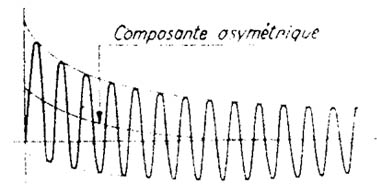
Tracemos las tres componentes asimétricas en escala semilogarítmica, las corrientes han sido llevadas en escala logarítmica. Extrapolando las curvas justo para el tiempo cero, y se obtienen así los tres valores iniciales.
Designémolos por a, b, c (ver figura 1144 - Medida de la reactancia subtransitoria. Diagrama de componentes simétricas de la corriente de cortocircuito). Se llevan las tres componentes según tres direcciones decaladas 60° y que parten del punto O, el mayor de los tres valores se lleva sobre la línea media. Se trazan las perpendiculares a cada extremidad de los tres vectores. Su punto de encuentro determina el punto M.
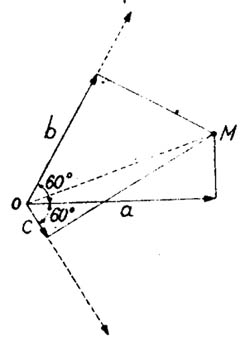
En el caso de que las perpendiculares no se encontraran en un sólo punto sino formaran un pequeño triángulo, se tomará como M el centro del triángulo OM representa la mayor componente asimétrica posible en la misma escala que las tres componentes radiales.
Se tiene x''d = e / OM siendo e la tensión en vacío de la máquina existente inmediatamente antes del cortocircuito, expresado en valor unitario.
La corriente representada por OM será expresada igualmente en valor unitario, la corriente normal de la máquina será tomada como unidad.
3er. método (método estático)
Una tensión monofásica E se aplica sobre dos ramas del arrollamiento trifásico (a 120 grados eléctricos) con el inductor en cortocircuito. El rotor está ubicado en una posición angular tal que la corriente inducida en los inductores i sea máxima.
En este momento, la máquina se encuentra en la posición axial para lo cual los inductores abrazan el flujo máximo que sale del estator.
Se tiene X''d = E / 2 Id (figura 1145 - Medida de la reactancia subtransitoria. Método estático) siendo Id la corriente en el inducido.
Si se ubica el rotor en la posición de corriente mínima para los inductores, se encuentra entonces en posición transversal, la corriente I de inducido será It y entonces la reactancia subtransitoria transversal X''t = E / 2 It
Reactancia inversa xi
1er. método
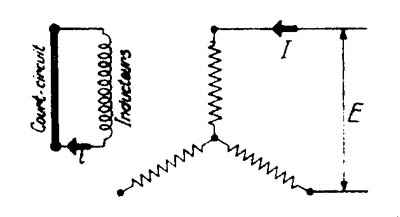
La máquina conectada en estrella es mantenida a la velocidad normal con dos bornes puestos en cortocircuito permanentemente (figura 1146 - Medida de la reactancia inversa).
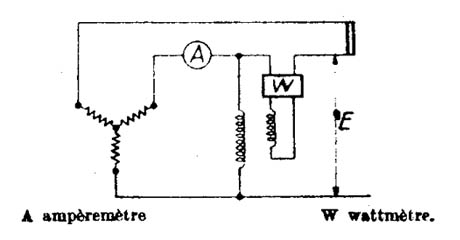
Se mide la corriente de cortocircuito y la tensión entre las dos fases cortocircuitadas y el extremo de la fase abierta. Se obtiene para esta impedancia
Zi = E / I Ö 3
Si E está expresada en valor unitario así como I, Zi es asimismo obtenida en valor unitario.
Se tendrá Xi = Zi sen j siendo j el ángulo de decalaje medido con ayuda del wattímetro.
Nota:
La presencia de armónicas puede influir en los resultados dados por este ensayo. En el ensayo de máquinas sin amortiguadores es bueno registrar oscilogramas además de la lectura del wattímetro. En este ensayo, si se debe hacer en turboalternadores el hecho de vigilar el rotor para controlar el calentamiento exagerado puede ser necesario operar con una corriente pequeña.
2do. método (dicho de Fallou)
Utiliza dos características en cortocircuito a) trifásica b) monofásica entre dos ramas.
- a - trifásica si se ha designado con U la tensión estrella normal (medida sobre la recta de la característica de entrehierro) e Icct la corriente de cortocircuito en conexión trifásica Icct = U / xd
- b - en monofásico (dos ramas)
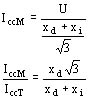
Se encuentra finalmente que
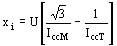
Este método es impreciso ya que los dos términos que deben restarse son muy próximos el uno del otro (compárese con el ejemplo numérico en D 482 - 18)
3er. método
Nosotros hemos visto que
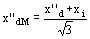
y determinamos x''dM por un ensayo de cortocircuito brusco entre dos fases. Si I''dM es la corriente de cortocircuito simétrica obtenida y U la tensión sobre la fase en vacío antes de la puesta en cortocircuito brusco, nosotros tenemos:
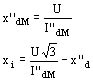
Reactancia homopolar
Método de las tres características en cortocircuito
Recordemos que la reactancia sincrónica monofásica (según el eje directo) y de línea a línea xdM resulta
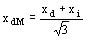
La reactancia sincrónica monofásica, entre línea y neutro según el eje directo xdN resulta
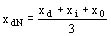
Si designamos con U la fuerza electromotriz en vacío que, para una misma corriente de excitación, dando en cortocircuito las corrientes IccM e IccN se tendrá
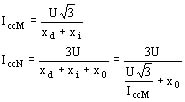
De estos cálculos
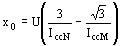
La corriente IccN contiene siempre una armónica 3ª muy importante, y es indispensable determinar la amplitud del término fundamental de la corriente, para introducirla en la fórmula que da x0.
Método de cortocircuito doble entre fase y neutro
Se determina la tensión Ea existente en bornes de la fase libre y se lee IN corriente que fluye entre los extremos B y C en cortocircuito que se dirige hacia el punto neutro (figura 1147 - Medida de la reactancia homopolar. Método de cortocircuito doble entre fase y neutro).
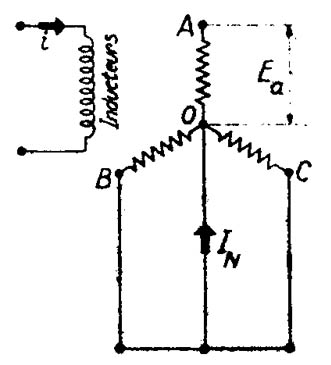
Por el método dicho de componentes simétricas se puede demostrar que con tal esquema la tensión sobre la fase abierta Ea resulta
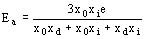
y la corriente que se dirige hacia el neutro es
IN = 3 i0
Siendo e la tensión (línea neutro) generada en la fase cuando la máquina no está cortocircuitada entre B, C y O, la corriente de excitación es la misma que se tiene después del cortocircuito, i0 es la corriente homopolar (compárese D 480 - 24 y D 120) x0, xd, xi las reactancias de la máquina definidas precedentemente. Resulta finalmente
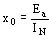
El método es muy simple porque se reduce a leer una tensión y una corriente.
Se hace notar que algunos calentamientos locales exagerados pueden producirse si las corrientes son demasiado elevadas o si no se conduce el ensayo con rapidez.
Método directo
La máquina es mantenida a velocidad nominal con los inductores en cortocircuito.
Todas las fases están conectadas en serie (figura 1148 - Medida de la reactancia homopolar. Método directo) y una tensión monofásica es aplicada en las extremidades libres. Se lee la tensión y la corriente a fin de obtener una característica E = f(I) que se extrapola hasta la corriente nominal, y más allá (si E e I son valores unitarios se tendrá x0 igualmente en valor unitario).
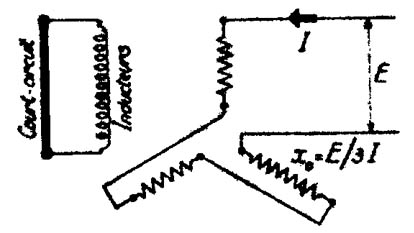
Es a la vez más indicado acoplar las fases en paralelo. La tensión es entonces un tercio de la requerida con la conexión serie precedente, y la corriente el triple. Las conexiones en cada caso deben ser tales que en todo momento las corrientes circulen en la misma dirección, después de los bornes de línea. Prácticamente los resultados son los mismos con el rotor detenido o asimismo sin rotor en toda la máquina.
Nota:
Por las reactancias xdM, x'dM, x''dM, xdN, x'dN, x''dN los mismos métodos operatorios que en trifásica se emplean en cortocircuito brusco, se efectúan tanto en monofásico entre dos bornes, como en monofásico entre un borne y el neutro.
Para xr, xkd, xkt no existe método normalizado y se acepta generalmente adoptar los valores calculados.
Medición de las principales constantes de tiempo
Constantes de tiempo de inducido, bajo un cortocircuito brusco ts
Es el tiempo (en segundos) necesario para que la componente asimétrica de la corriente inducida provocada por un cortocircuito brusco (la máquina girando a su velocidad normal) decrece a 0.368 veces su valor inicial (la ley de decremento de la corriente sigue una ley exponencial y 0.368 = 1 / e siendo e la base de logaritmos neperianos); ts se deduce del ensayo de cortocircuito brusco cuando se presenta una componente asimétrica (compárese fig. 79 en D 482).
La línea media de las ondas oscilográficas se lleva en papel semilogarítmico.
Se dice que esta constante de tiempo se refiere a la componente continua, mientras dura este fenómeno, la onda de corriente, no es simétrica en relación a la línea de abscisas.
Constante de tiempo subtransitoria t''d
Es el tiempo en segundos, necesario para que la componente del decremento rápido (subtransitorio) de la corriente de inducido durante los primeros ciclos siguiendo el eje directo después de un cortocircuito brusco trifásico (la máquina gira a su velocidad nominal) cae a 0.368 veces el valor inicial (0.368 = 1/e siendo e la base de logaritmos neperianos).
Se deduce t''d del ensayo de cortocircuito (compárese D 482 - 19).
Se debe subrayar que el cálculo de esta constante de tiempo que hace intervenir los circuitos amortiguadores, es frecuentemente muy delicada debido a la naturaleza compleja de ellos. Por otra parte el amortiguamiento por piezas de hierro macizas (caso del turboalternador) no conduce a exponenciales puras, y no permite definir con precisión las constantes de tiempo.
En general para los turboalternadores, no se dan garantías más que sobre constantes de tiempo transitorias.
Constante de tiempo transitoria t'd
Este es el tiempo en segundos requerido para que el valor eficaz de la componente de corriente inducida, que decrece lentamente (transitorio) en caso de cortocircuito brusco trifásico decrece a 0.368 veces su valor inicial (la máquina gira a su velocidad nominal).
Se deduce t'd del ensayo de cortocircuito franco (compárese D 482 - 19)
Nota:
Para obtener los valores habitualmente especificados de las constantes de tiempo t'd y t''d que corresponden a un cortocircuito brusco corriente ejecutado a partir del funcionamiento a tensión nominal, los valores deducidos del ensayo a tensión reducida (se adopta generalmente la semitensión) deben ser afectados de coeficientes correctivos para tener en cuenta el grado de saturación.
Constante de tiempo de inductores el alternador está en vacío t'd0
Esta constante de tiempo t'd0 es el tiempo necesario en segundos para que el valor eficaz de la componente de la tensión de inducido que decrece lentamente (transitorio) a circuito abierto caiga a 0.368 veces el valor inicial cuando el arrollamiento inductor es bruscamente cerrado en cortocircuito (la máquina rota a velocidad nominal).
Se toma un oscilograma de la tensión de inducido y además la corriente y tensión de inductor. La tensión residual es sustraída del valor dado por el oscilograma, y el resultado llevado en función del tiempo utilizando, para la tensión, una escala logarítmica.
Los puntos caen sensiblemente sobre una recta y los primeros puntos a decremento rápido se desprecian. El intervalo de tiempo representado por el segmento comprendido entre el punto de intersección de la recta con el eje (t=0) y el punto en el cual sobre esta recta se presenta 0.368 veces la tensión inicial, da la constante de tiempo requerida.
Constante de tiempo subtransitoria a circuito abierto según el eje directo
Esta constante de tiempo es deducida del ensayo precedente y no considera más que términos de decremento rápido (subtransitorio) obtenidos descontando punto por punto al valor de la tensión, la parte transitoria de esta.
Funcionamiento asincrónico de un motor sincrónico monofásico
Según el eje longitudinal
En caso de funcionamiento asincrónico el diagrama equivalente, (figura 1177 - Funcionamiento como asincrónico de un motor sincrónico monofásico. Diagrama según el eje longitudinal) se compone de dos partes I y II. La primera parte se refiere al sentido normal del campo rotante con deslizamiento g y la segunda parte II se refiere al campo inverso de deslizamiento (2-g).
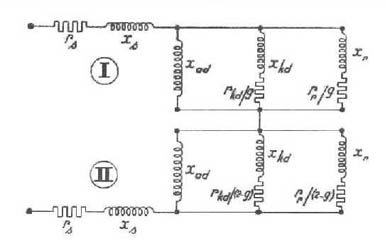
En el diagrama equivalente, según el eje transversal nosotros hallamos igualmente dos partes, una corresponde al campo directo y otra al campo inverso.
Nosotros podemos entonces formar sucesivamente las admitancias Yrd e Yrdi por una parte e Yrt e Yrti por otra parte.
Para la parte I según el eje directo tenemos:
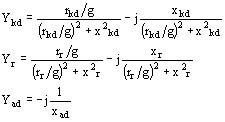
La suma de estas admitancias nos da
Yrd = E - jF
siendo E la suma de términos reales y F la suma de términos imaginarios. Tendremos entonces pasando a las impedancias:
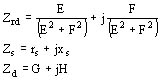
siendo G la suma de parte reales de Zrd y de Zs y H suma de las partes imaginarias de las mismas cantidades de donde
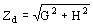
Para la parte II nosotros operamos igualmente y tendremos
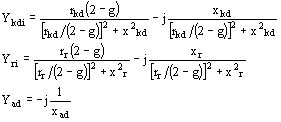
La suma de estas admitancias nos da Yrdi = K - jL
siendo K la suma de los términos reales y L la suma de los términos imaginarios. Nosotros tendremos entonces
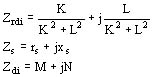
siendo M la suma de partes reales de Zrdi y de Zs y N la suma de las partes imaginarias de las mismas cantidades.
La impedancia total correspondiente al diagrama equivalente según el eje directo será la suma de Zd y de Zdi.
Si nosotros queremos calcular la corriente tomada por el motor tendremos
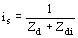
en valor unitario. Nosotros calcularemos el par correspondiente al deslizamiento g con la fórmula
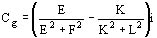
El par debido al campo inverso se resta aritméticamente de el par debido al campo directo.
Según el eje transversal
El diagrama equivalente (figura 1178 - Funcionamiento como asincrónico de un motor sincrónico monofásico. Diagrama según el eje transversal) se compone igualmente de dos partes III y IV y podemos escribir para III siguiendo el mismo camino precedente
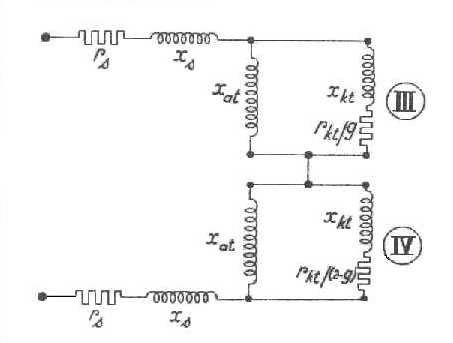
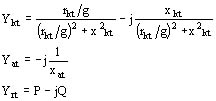
siendo P la suma de las partes reales de Ykt y de Yat, y Q la suma de las partes imaginarias de las mismas cantidades.
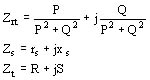
siendo R la suma de las partes reales y S la suma de las partes imaginarias
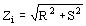
Para la parte IV tenemos:
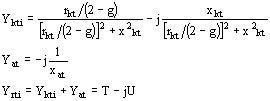
siendo T la suma de las partes reales de Ykti y de Yat y U la suma de las partes imaginarias de las mismas cantidades.
Pasando a las impedancias:
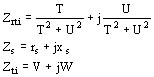
siendo V la suma de las partes reales de Zrti y de Zs y W la suma de las partes imaginarias de las mismas cantidades donde 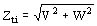
La corriente absorbida por el motor será en valor unitario
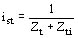
y el par correspondiente:
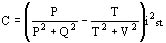
Indice bibliográfico
- Synchronous machines reactances. General Electric rev. nov. 1932.
- (Formule simple pour le calcul de la dispersion dans les encoches). Elektrotechnik Maschinenbau, fevr. 1930.
- (Décréments et valeurs numériques de xd, x'd, x''d). Electric j. mars 1923. Annexe 3. - G.M.E. 1524 de la Chambre syndicale des constructeurs de gros matériel électrique.
- P.L. ALGER - The calculation of the armatures reactance of syncrhonous machines. Trans. A.I.E.E. avr. 1928.
- M. BARRERE - Calcul des réactances des machines syncrhones. Bull. S.F.E. nov. 1932.
- M. BARRERE - Calcul de la courbe de courant de court-circuit triphasé, d'alternateurs en fonction du temps. R.G.E. XXX, nº 16.
- L.CARPENTIER et G. RUELLE - Analyse du fonctionnement asynchrone des machines à pôles sailants, à l'aide d'un calculateur électronique numérique. Rev. d'electr. et de mécan. Alsthom, avr-mai-juin 1957.
- DALTON et CAMERON - (Mesure des réactances subtransitoires et de la réactance inverse des machines syncrhones à pôles sailants). A.I.E.E. août. 1952.
- E. DRIEST - Dispositif d'excitation des machines syncrhones avec réglage de tension par amplidyne. A.E.G. Mitt. nºs 5 ,6 mai-juin 1957.
- C. I. FORTESCUE - Method of cinetical coordinates applied to the solution of polyphase networks. Trans. A.I.E.E. 37 1918.
- L. A. KILGORE - Calculation of syncrhonous machines constants. Trans. A.I.E.E. déc. 1931.
- R. LOYES - Réactances et constantes de temps des machines syncrhones. Rev. Jeumont, juil-sept 1950.
- R.H. PARK et B.L. ROBERTSON - The reactance of syncrhonous machines. Trans. A.I.E.E. avr. 1928.
- A.W. RANKIN - Per unit impedances of synchronous machines. Trans. A.I.E.E. mars-oct-dec. 1945.
- R.L. RUSSEL et K.H. NORSWORTHY - A statorfed half-speed syncrhonous motor. Proc. I.E.E. (Part A) nº 13, fev 1957.
- A. STILL - Reactance of syncrhonous machines. Trans. A.I.E.E. juil 1930.
- S.B. TONIOLO - Contribution à l'étude des réactances synchrones. Electtrotecnica 8 bis. sep 1949.
- J.C. WHITE - Synchronous-motors starting perfomance calculation. Trans. A.I.E.E. nº 25 août 1956.
- S.H. WRIGHT - Determination of synchronous machines constants by test. Trans. A.I.E.E. 50 1931.
- Publicaciones Alsthom citadas en el texto D 120, D 420, D 480, D 482, D 510, D520

Copyright 2008 - 2012 INDUCOR INGENIERIA S.A. | Todos los derechos reservados | CCS | HTML



