Advanced
Cable Testing
CALCULO Y DISEÑO DE MAQUINAS ELECTRICAS
APENDICE 16 - CAMPOS MAGNETICOS
2.1 CAMPO MAGNETICO DEBIDO A CORRIENTE ELECTRICA
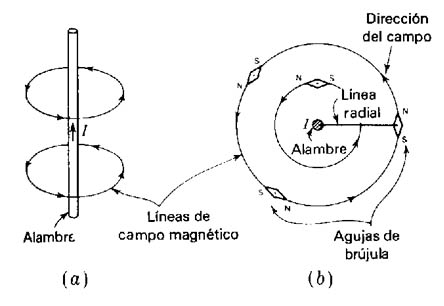
Ustéd observó que alrededor de un alambre que conduce corriente (eléctrica estacionaria) se presenta un campo magnético (estático), B desde ya llamémoslo densidad de flujo magnético. Si se siguen las líneas de campo se rodea al conductor que transporta corriente (Figura 901)(a) Campo magnético alrededor de un alambre (b) Sección transversal perpendicular al alambre).
Faraday observó que si se tiene un campo B uniforme, sobre un trozo de conductor por el que circula cierta corriente se presenta una fuerza motora o motriz:
dF = B ´ I.dl (1)
La fuerza es máxima cuando la densidad de flujo magnético representada por el vector B es perpendicular a I, el producto es vectorial (debe definirse una terna de ejes en el espacio).
La ley de Biot-Savart y Laplace permite determinar la densidad de flujo magnético B debida a la corriente en un conductor.
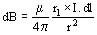(2)
Siendo r1 el versor de r, el producto de r1 con I.dl es vectorial, de donde integrando:
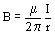
En el aire la permeabilidad es:
m 0 = 400 p 10-9 (H / m) (3)
En un medio cualquiera:
m = m relativo m0 (4)
La densidad de flujo magnético B debida a la corriente alrededor de un alambre rectilineo infinito (Figura 902) (Campo magnético creado por la corriente que circula en un elemento dx de un largo conductor rectilíneo) puede ser determinada, usando la analogía con el problema ya resuelto del conductor cargado para el que se tiene:
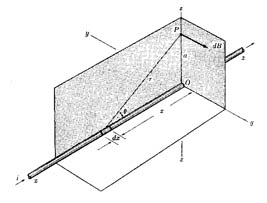
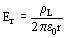resulta entonces 
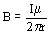(5)
Entre dos conductores paralelos (infinitos) puede calcularse la fuerza (si las corrientes son en sentido contrario, de repulsión) por unidad de longitud:
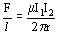(6)
La densidad de flujo magnético representada por B, (ver la analogía con el campo eléctrico y la densidad de flujo eléctrico), está dada por:
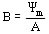(7)
siendo Ym el flujo magnético a través del área A.
Se puede pensar en tubos de flujo magnético, a diferencia del campo eléctrico que inicia y termina en cargas, los tubos de flujo magnético son continuos, cerrados, piénsese en los tubos de flujo que rodean a una línea de corriente, o bien un anillo con corriente.
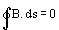(8)
El campo magnético es solenoidal, esta es una diferencia fundamental con el campo eléctrico estático, que es laminar.
Para el flujo magnético también puede considerarse la ley de Gauss, flujo a través de una superficie cerrada.
Divergencia B = 0 (9)
El campo magnético de una espira por la que circula corriente, es un problema particularmente interesante, ya que este modelo se presenta especialmente en las máquinas eléctricas, un planteo general determina la torsión sobre la espira y aparece el concepto de momento magnético (Figura 903) (Espira rectangular en campo uniforme B experimenta un momento torsor que tiende a alinear su normal con B):
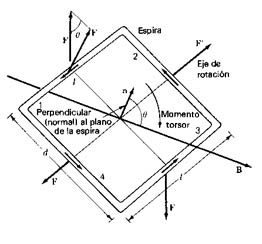
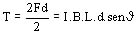(10)
siendo J el ángulo entre la normal al plano de la espira y B, y L.d el área.
El momento de torsión es proporcional a la corriente en la espira y a su área.
Veamos ahora sólo casos particulares de valor de la densidad de flujo en un punto. Para una espira circular (Figura 904) (Campo magnético creado por un elemento dl de una espira circular de conductor que transporta corriente), sobre el centro de la espira se presenta:
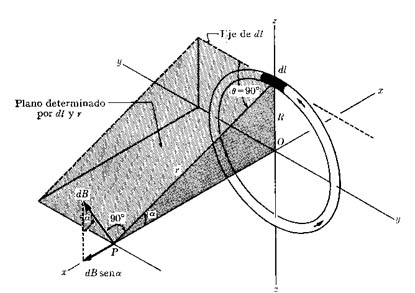
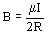(11)
siendo R el radio de la espira, I la corriente.
Si se determina la densidad de flujo dentro de una bobina solenoidal se obtiene, para el centro del solenoide (Figura 905) (Lámina de corriente equivalente del solenoide):
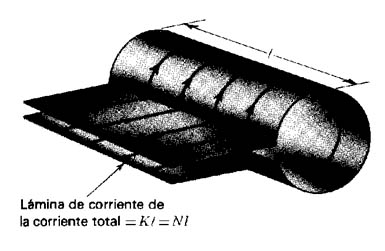
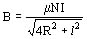(12)
siendo N espiras, R radio, l longitud, NI lámina de corriente.
Si l >> R se tiene
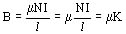(13)
Siendo K la densidad de corriente pelicular del solenoide (densidad lineal de corriente), equivalente a una sola vuelta de lámina conductora con corriente uniformemente distribuida.
Si se hace la misma determinación para el extremo del solenoide el resultado es la mitad, pueden compararse estos resultados con los dipolos eléctricos y desarrollar alguna analogía.
La inductancia de un solenoide es:
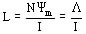(14)
siendo L el flujo de acoplamiento total, y Ym el flujo.
Esta definición es válida para el aire, pero no es aplicable a los medios ferrosos, porque su permeabilidad no es constante, en medios no lineales se define la inductancia incremental.
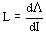
Con la relación 14 se pueden resolver inductancias de geometrías simples, por ejemplo un toroide (Figura 906) (Toroide):
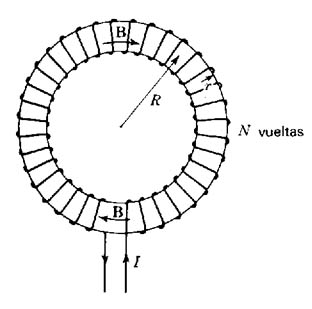
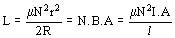(15)
siendo r el radio de la bobina y R el radio del toro.
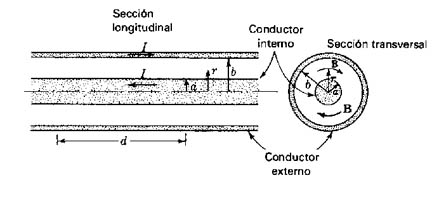
Para un conductor coaxial se puede determinar la inductancia por unidad de longitud (Figura 907) (Línea coaxil de transmisión):
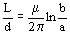(16)
siendo a el radio del conductor interno y b el radio del tubo externo.
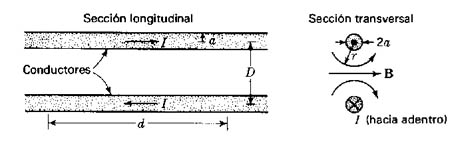
Para dos conductores paralelos la inductancia resulta (Figura 908) (Línea bifilar de transmisión):
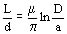(17)
siendo a el radio de los conductores y D la distancia entre ellos.
La ley de Ampere dice que:
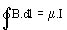(18)
Esta ecuación se hace independiente del medio introduciendo el concepto de H que llamaremos propiamente campo magnético (obsérvese la analogía con el campo eléctrico, intensidad del campo eléctrico).
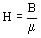(19)
siendo m la permeabilidad del medio.
Se destaca que al estudiar el campo eléctrico se partió de E y se llegó a D, para el campo magnético se partió de B y se llegó a H.
La ley de Ampere puede expresarse como a continuación se indica, y se puede calcular como varía el campo dentro de un conductor, abrazando más y más corriente.
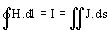(20)
Se hace conveniente repasar similitudes y diferencias para establecer las analogías entre campos eléctrico y magnético, presentamos las fórmulas de a pares para evidenciar la correspondencia entre campo eléctrico y campo magnético:
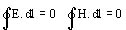(12)
el campo magnético no encierra ninguna corriente, la trayectoria de integración evita las corrientes.
El campo eléctrico es laminar, se deduce de una función escalar potencial V, el campo magnético no es laminar, porque sus líneas de flujo forman circuitos cerrados, pero en la región libre de corrientes (donde no encierra ninguna corriente) puede ser tratado como laminar:
Ñ V = - E Ñ U = - H (23)
El campo magnético H se puede en este caso obtener de un potencial magnetoestático escalar U, que tiene dimensiones de corriente (y se expresa en Amperes).
El campo eléctrico, cuando hay fuerzas electromotrices en la trayectoria de integración y el campo magnético (si la trayectoria encierra corriente, una o N veces, N´ I=FMM llamada también fuerza magnetomotriz) valen:
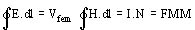(24)
Para resolver el problema de determinar el potencial magnético del campo creado por un alambre conductor se interrumpen las trayectorias circulares alrededor del conductor (Figura 909) (Integral de línea de H alrededor de trayectorias cerradas (a) y (b) igual a la corriente (c) y (d) igual a cero), con un plano entre el conductor y el infinito, a un lado de este plano el potencial magnético U = 0, y al otro lado U = I, es fácil ahora encontrar los planos equipotenciales intermedios, con trayectorias de integración que no encierran corrientes.
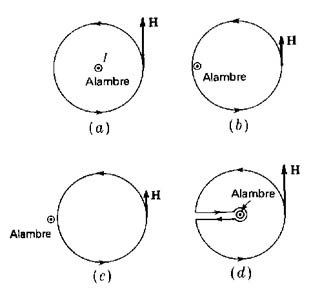
Al insertar el plano se ha transformado el espacio en simplemente conexo, y el problema es análogo a las regiones libres de carga del campo eléctrico:
Ñ D = 0 Ñ B = 0
Ñ2 V = 0 Ñ2 U = 0
Cuando la región es libre de corrientes, y la trayectoria no es cerrada, el potencial magnético escalar y la fuerza magnetomotriz, son una misma cosa.
Introduzcamos ahora el concepto de celdas de campo y permeabilidad, pensemos en una línea de transmisión de dos cintas conductoras planas paralelas de ancho w separadas l , las corrientes iguales y contrarias, la inductancia es (Figura 910) (Línea de transmisión de cintas paralelas (a) en perspectiva (b) sección transversal (c) celda de campo magnético):
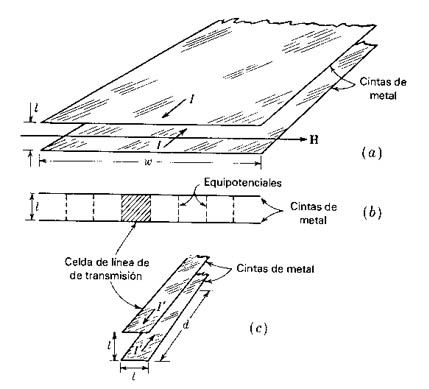
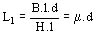(25)
La inductancia por unidad de longitud
L1 / d = m (26)
Obsérvese la analogía con las celdas del campo eléctrico y el campo de corrientes (ver fórmulas 27 y 42 del Apéndice 1).
En la teoría de circuitos tiene sentido para una trayectoria cerrada que encierra la corriente I, la ley de Amper expresada por la fórmula (20):
Si dividimos ambos miembros por el área encerrada por el contorno, y hacemos el límite para el área tendiendo a cero, reduciendo el camino de la integral, llegamos al concepto de rotor (rotacional) y densidad de corriente J (Figura 911) ((a) Densidad de corriente como el límite de la razón D l a D s (b) Construcción para encontrar la componente x del rotacional de H):
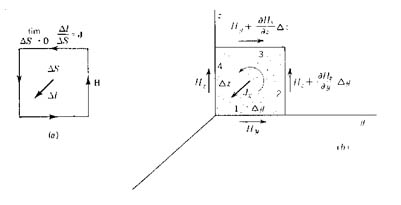
Rotor H = J (27)
El rotor esta dado por el producto vectorial del operador Ñ por el vector H.
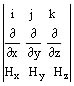
Externamente a los conductores se tiene que no hay corriente y entonces:
Rotor H = 0 (28)
Repasemos un poco las operaciones sobre escalares y vectores que se han introducido hasta ahora:
- Gradiente (Ñ ) opera sobre una función escalar y da una función vectorial.
- Divergencia (Ñ ) opera sobre una función vectorial para dar una función escalar.
- Rotor, rotacional (Ñ vectorial) opera sobre una función vectorial para dar otra función vectorial.
El campo vectorial con divergencia muestra variación a lo largo del campo (en la misma dirección), en cambio el campo vectorial con rotor muestra variación normal a la dirección del campo.
El operador Ñ es un operador vectorial, pero técnicamente no goza de las propiedades de un vector propiamente dicho, porque en rigor goza de propiedades vectoriales y diferenciales, estas últimas se manifiestan cuando el operador se aplica reiteradamente.
La divergencia del gradiente Ñ (Ñ f) aplicada a un escalar da una función escalar y recibe el nombre de Laplaciano Ñ2 = D
El gradiente de la divergencia aplicado a un vector Ñ (Ñ A) da un vector, esta operación no debe confundirse con la que sigue (cuyo resultado es distinto).
El Laplaciano aplicado a un vector D A da un vector, esta operación es análoga a aplicar el Laplaciano a las tres componentes del vector (no debe confundirse con el gradiente de la divergencia).
La divergencia de un rotacional (de una función vectorial) es cero
Ñ (Ñ ´ A) = 0
El rotacional del gradiente es cero
Ñ ´ (Ñ A) = 0
Se demuestra que el rotor del rotor cumple la siguiente identidad vectorial:
Ñ ´ (Ñ ´ A) = Ñ (Ñ A) - Ñ2 A
en palabras gradiente de la divergencia menos el Laplaciano.
Un campo vectorial cuyo rotor es nulo tiene un potencial escalar que lo genera.
Si un campo vectorial no tiene rotacional es laminar, los hilos de flujo son discontinuos, van de fuente a sumidero.
Un campo vectorial cuya divergencia es nula es un campo solenoidal, los tubos de flujo no tiene fuentes ni sumideros.
Para el campo magnético se ha visto que la divergencia de B es cero, entonces debe existir una función A cuyo rotor es B, A es el llamado potencial vectorial o vector potencial.
B = rotor A (29)
rotor de rotor de A = rotor de B = m . J
-Ñ2 A = Ñ ´ B = m . J
Observemos además que:
Divergencia D = r
encuentra las fuentes r del campo eléctrico.
Rotor H = J
encuentra las fuentes J del campo magnético.
Partiendo del potencial vectorial A con el rotor se determina la densidad de flujo B cuyo rotor esta relacionado con m . J.
La Densidad de flujo magnético en un punto esta dada por:
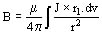
siendo J ´ r1 producto vectorial
Surge de las relaciones establecidas:
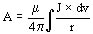
Mientras que el potencial escalar V del campo eléctrico, y el potencial magnético escalar U, tienen un significado físico claro y simple, el potencial vectorial no lo tiene, se debe considerar sólo como una abstracción matemática, pero que ayuda a encontrar solución a un problema.
2.2 CAMPO MAGNETICO DEBIDO A ESPIRAS CON CORRIENTE
Se ha determinado el campo magnético debido a espiras en algunos puntos particulares, como ser el centro de la espira, el centro de la bobina, el extremo de la bobina.
Pero es de interés conocer en otros puntos del espacio la densidad de flujo B debida a una espira, o a varias espiras, y para resolver este problema se ha desarrollado un programa basado simplemente en las fórmulas que describen la ley de Biot-Savart y Laplace.
El programa se llama "CAMPOB" y desarrolla el cálculo de la densidad de flujo B debido a bobinas cilíndricas coaxiales, pensemos por ejemplo en los arrollamientos de un transformador.
La bobina o las bobinas se consideran formadas por espiras separadas paralelas al plano XY con su eje sobre el eje Z.
El plano de estudio es el XZ, suficiente por razones de simetría, y se determina la densidad de flujo B en un rectángulo definido por sus coordenadas extremas.
La bobina se divide en trozos de amplitud angular DALFA y estos trozos elementales se rectifican sobre la tangente, para lograr una representación perfeccionada el ángulo se reduce, los primeros tanteos se pueden hacer con 30 o 45 grados, luego se reduce a 10 grados que parece suficiente para una excelente aproximación.
Se describen varias espiras, con corriente, con signo ± para definir su sentido, si se representa un transformador, las espiras primarias y secundarias tendrán corrientes de sentidos opuestos, el núcleo no estará representado.
Para cada punto del plano XZ, y para cada espira se determina la densidad de flujo B (tridimensional, pero que es bidimensional por simetría cilíndrica)
El campo en el punto XZ se calcula por acumulación de valores debidos a cada trozo de espira, no olvidemos que el campo es tridimensional (y así lo calcula el programa) aunque el resultado es bidimensional.
Para cada espira, y para cada trozo que cubre el ángulo elemental se determina el producto:
DLA = RES ´ DALFA ´ COR
siendo RES el radio de la espira, DALFA el ángulo, COR la corriente, y el resultado DLA representa el trozo de conductor con corriente.
Se determina la distancia entre trozo de espira y punto espacial de cálculo RRR, su módulo y finalmente se hace el producto vectorial
DLA ´ RRR
Que debe dividirse por el modulo de RRR al cubo, obteniéndose el campo debido al trozo de conductor.
El método parece trabajoso, pero el programa es simple de entender, por lo que permite fáciles modificaciones para adaptarlo a necesidades particulares.
Se puede obtener la densidad de flujo B en un plano que pasa por el eje de las bobinas, conviene observar este campo en sus dos componentes, paralelas al eje X, radial, y paralela al eje Z, axial, un conductor con corriente normal al plano y sumergido en ese campo sufrirá fuerza axial debida al campo radial, y fuerza radial debida al campo axial.
Como es de interés determinar la fuerza que sobre una espira hacen todas las restantes, inclusive ella misma, cuando se calcula el campo en un punto debido al trozo de espira que pasa por el mismo punto este trozo se quita del modelo, ya que un trozo de espira no provoca campo que haga fuerza sobre el mismo, se evita así también el problema de cálculo numérico que aparece siendo nulo el valor de RRR.
Los resultados de estos cálculos pueden graficarse, y para esto se ha desarrollado el programa "BCAMPO", a cada punto corresponden dos valores del campo magnético, radial y axial, que dan su orientación, pudiendo graficarse el vector (observándose que decrece rápidamente al alejarse de las bobinas).
Para representar el campo es más claro trazar en cada punto las rectas según la dirección del campo, y la normal, sobre este mapa es fácil trazar líneas de campo y equipotenciales si hay interés.
2.3 CAMPO MAGNETICO CON MATERIALES FERROMAGNETICOS
Alrededor de un alambre que conduce corriente se presenta un campo magnético, y también alrededor de un imán (circuitos microscópicos), o una barra de hierro magnetizada por un solenoide (circuitos macroscópicos).
Entre un imán y un solenoide se nota cierta equivalencia, y en analogía con el dipolo eléctrico se puede definir un dipolo magnético.
Debe notarse que los polos magnéticos no pueden aislarse como se hace con los polos eléctricos, esta es la diferencia importante.
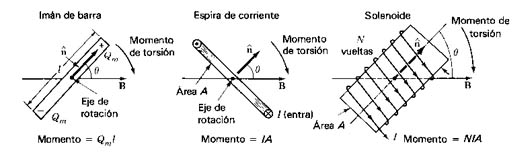
Sobre un imán puesto en un campo magnético B uniforme se presenta un momento de torsión:
T = Qm B l sen J
siendo Qm intensidad polar, B campo magnético, F = Qm B fuerza, Qm l momento angular, l longitud del dipolo, teta ángulo entre B y el eje del dipolo.
Se puede lograr una fórmula análoga para un solenoide donde el momento magnético es:
Qm l = N I A = m
donde N I es la corriente laminar, A el área del solenoide.
El momento de torsión tiende a alinear m con B (Figura 937) (Imán de barra (dipolo magnético), espira de corriente y solenoide en un campo uniforme), este momento puede medirse sumergiendo el objeto magnético B y midiendo la torsión (no es necesario llegar a determinar Qm y l).
Recordemos el concepto de permeabilidad relativa que es la relación entre la permeabilidad del material magnético y la del vacío.
Son valores característicos de la permeabilidad relativa de los materiales ferromagnéticos: 2000 para el acero, 5000 para el hierro y 7000 para el hierro silicio.
La permeabilidad relativa de las substancias ferromagnéticas es variable y presenta un valor máximo, nótese que la permeabilidad relativa depende del campo aplicado, el máximo se presenta para distintos materiales para distinto valor de campo.
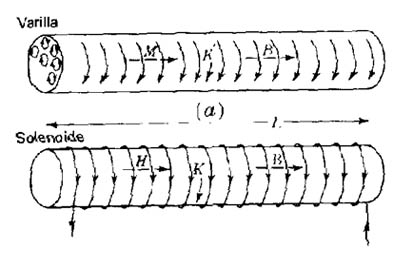
Se puede observar la equivalencia entre una barra uniformemente magnetizada y un solenoide (Figura 938) ((a) Varilla uniformemente magnetizada (b) solenoide equivalente).
En el centro del solenoide
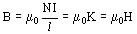
siendo K la densidad de corriente pelicular.
En el centro de la barra:
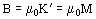
siendo K' la densidad de corriente pelicular equivalente.
A los vectores magnéticos B y H se ha agregado M que también tiene la dirección de B.
Considérese un toroide de aire de área A, radio R, N0 vueltas:
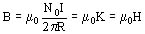
poniendo el mismo devanado sobre un anillo de hierro B aumenta, si en lugar del anillo de hierro queremos conseguir lo mismo deberemos poner Nm espiras (Figura 939) (Toroide con N0 vueltas que produce B0 y Nm vueltas que produce Bm) de manera que:
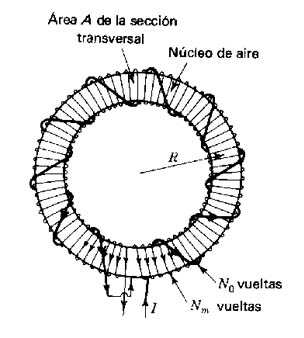
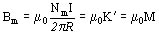
Entonces:
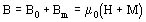
En medios isotrópicos M y H tienen la misma dirección, como Ñ B = 0 resulta Ñ H = -Ñ M, la lectura de esto es que el campo H inicia donde termina M y viceversa.
Rotor B = m0 rotor H + m0 rotor M
Rotor B = m0 (J + J')
siendo:
J densidad real de corriente
J' densidad equivalente en la superficie de la barra magnetizada.
En la frontera entre medios m1 y m2 las componentes tangenciales de H son las mismas a ambos lados de la frontera
Ht1 = Ht2
El campo magnético tangencial es continuo a lo largo de la frontera entre dos medios.
Puede existir un campo finito en la frontera se presenta una película de corriente en la superficie de discontinuidad, en este caso:
Ht1 - Ht2 = K
siendo K densidad lineal de corriente que fluye en una lámina infinitesimal (delgada) en la superficie.
Por otra parte:
Bn1 = Bn2
Siendo a1 y a2 los ángulos de incidencia del campo en la frontera (Figura 940) (Frontera entre dos medios de diferente permeabilidad), se tiene:
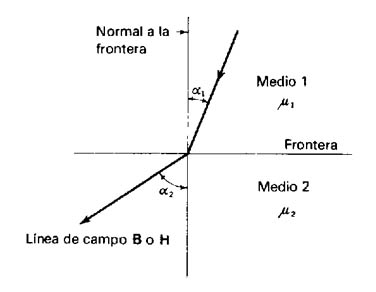
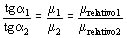
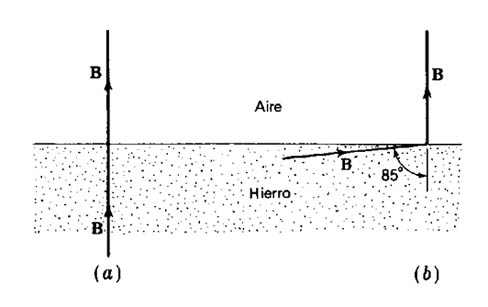
Con estas reglas se observa como se quiebran las líneas de campo al pasar de un medio a otro, entre hierro y aire la relación es 7000, si a1 es cero también lo es a2, la línea de campo perpendicular no se quiebra, pero si a1 es sólo 0,1 grado a2 es 85 grados, casi 90, (Figura 941) (Líneas B en frontera aire-hierro) esta es una diferencia muy apreciable respecto de las condiciones reales de los campos eléctricos y de corriente análogos.
La lámina de corriente permite eliminar uno de los medios, haciendo:
Ht1 = K2
y el estudio se concentra sólo en el medio 1 considerando K2.
El circuito eléctrico tiene analogía con el circuito magnético, veámosla:
siendo:
la reluctancia total
FT la fuerza magnetomotriz total
Ym el flujo en el circuito magnético
El recíproco de la reluctancia es la permeancia:
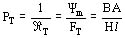
El campo puede dividirse en elementos de permeancia:
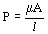
la analogía con G conductancia, y también con L y C es inmediata.
Lecturas recomendadas John D. Kraus, Electromagnetismo (Mc Graw Hill) sección 6-19 página 281 - trazado de mapas de campos magnéticos; celdas de campos magnéticos; 6-20 página 286 - comparación de mapas de campo en los casos eléctrico, magnético y de corriente.
Un circuito magnético con entrehierro requiere una cierta fuerza magnetomotriz para que aparezca cierta densidad de flujo en el hierro f y en el entrehierro e.
NI = Hf lf + He le
siendo H el campo y l la longitud.
Bf = Hf mf
Be = He m0
si el entrehierro es pequeño las áreas en las que se presenta el flujo son iguales, pero si el entrehierro es grande el efecto de bordes incrementa el área del mismo.
Bf Areaf = Be areae
Lectura recomendada John D. Kraus, Electromagnetismo (Mc Graw Hill) sección 6-26 página 297 - Comparación de campos estáticos eléctricos y magnéticos.
2.4 CAMPOS LIMITADOS Y LA ECUACION DE LAPLACE
Es necesario evaluar los campos que aparecen en los objetos de estudio, .es necesario trazar mapas con líneas de campo y equipotenciales que proporcionan información.
Los mapas de campo son soluciones de la ecuación de Laplace, se da la condición de unicidad, la solución de la ecuación de Laplace es única.
El planteo general del problema esta dado por la ecuación de Laplace, en algunos casos por la de Poisson, y por los valores de frontera.
En el pasado estos problemas se resolvían con modelos analógicos, cuba electrolítica, papel de resistencia, red de resistores.
El método de cálculo numérico se ha explicado ligado al programa "POTRES", el método propuesto que es iterativo (relajación) es demostrable a partir de la ecuación diferencial escrita en diferencias finitas.
La ecuación de Laplace se plantea para campos planos, para coordenadas cilíndricas y para coordenadas esféricas, algunos modelos analógicos fracasan, o su construcción se dificulta mucho.
2.5 METODO DE LAS IMAGENES
En algunos casos se dan condiciones que asocian la solución de un problema con dos medios a forzar condiciones de simetría, a través de la construcción de una imagen del campo.
Lectura recomendada John D. Kraus, Electromagnetismo (Mc Graw Hill) sección 7-14 página 338 - teoría de imágenes.
Ya se ha planteado el caso de una línea infinita de un solo conductor, cargada, sobre un plano metálico, que se estudia como bifilar.
Efectivamente si entre las dos cargas de la línea bifilar se introduce un plano metálico, y luego se quita una carga, nada cambia.
Otro problema es un conductor con corriente sobre un plano metálico que también se resuelve por el método de las imágenes como una línea bifiliar.
El método de las imágenes fue desarrollado por Lord Kelvin, sucesivamente lo vemos aplicado a campos eléctricos estáticos, campos de corrientes y a campos magnéticos producidos por imanes, y por corrientes que circulan en conductores, destacando particularidades que distinguen este último caso.
Este método permite encontrar el campo eléctrico de una carga ubicada al lado de una superficie plana conductora.
La superficie conductora (Figura 942) (de potencial nulo, produce una carga reflejada (imagen) igual y de signo contrario.
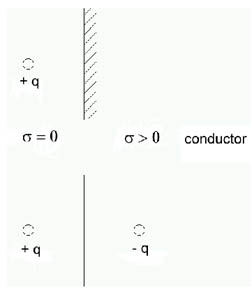
Entre las dos cargas (real e imagen) el plano medio es de simetría y resulta ser un plano equipotencial como requiere la física.
Sobre este plano conductor (metálico) aparece carga inducida por influencia de la carga real.
Una carga entre dos planos conductores paralelos plantea el caso de reflexiones múltiples, como cuando nos encontramos entre dos espejos paralelos.
La solución que se obtiene es válida dentro del espacio entre los planos, la cantidad de imágenes es infinita, pero en la aplicación se limita el número de imágenes consideradas.
Otro problema que se resuelve con este método es el campo que presenta una carga q1 en un medio e 1, donde más allá de una superficie plana se tiene un medio e2 (Figura 943).
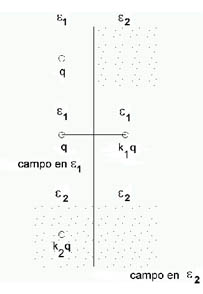
El campo en el medio e1 es el producido por la carga q agregando una imagen q1 = k1 q, siendo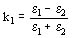 
y reemplazando el medio e2 por e1 .
El campo en el medio e2 es producido reemplazando la carga q por q2 = k2 q siendo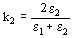 
, no hay imagen y se reemplaza el medio e1 por e2.
Estas propiedades se demuestran satisfaciendo en la superficie límite las condiciones a que obliga la física y que conducen a k1 + k2 = 1.
Un ejemplo interesante (Figura 944) propuesta en la bibliografía es una pared metálica, un dieléctrico e2 hasta cierta altura, y arriba otro e1, en este último una carga q.
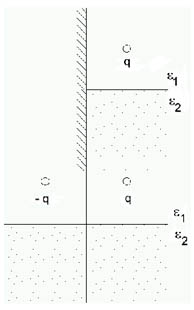
Para resolverlo primero se elimina la pared metálica, aparecen la imagen -q.
Luego se resuelve el problema entre los dos dieléctricos con el dipolo (q, -q) en e 1.
Obsérvese que k1 puede tener signo positivo e1 > e2 o negativo en caso contrario.
Según la ley de Culomb el medio conductor (donde E = 0) es equivalente a e2 tendiendo a infinito, k1 = 1 y se produce la reflexión.
Para los problemas de campos de corriente la analogía es inmediata.
Una aplicación interesante para observar es la dispersión de corriente en el suelo de cierta resistividad, considerando la superficie límite suelo aire como superficie de reflexión.
Por las características no homogéneas del suelo a veces se hace la hipótesis de considerar una capa superior de cierto espesor y resistividad y debajo un suelo de otra resistividad (mayor o menor).
Este es un complejo caso de reflexiones múltiples con factores que dependen de las resistividades (conductibilidades) de las capas.
El mismo método se aplica para resolver el campo magnético.
Un medio (aire) de permeabilidad m1 y un medio m2 , si en el medio m 1 se encuentra una barra imantada, se aplica el método de las imágenes reflejadas con analogía a lo que se hace para el campo eléctrico,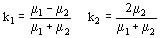 
.
Cuando en el medio en lugar de un imán se encuentra un conductor los factores son distintos de los considerados para las barras imantadas, y exactamente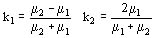 
pero el método es el mismo.
Esta diferencia se confirma controlando que se cumplen las condiciones de límites, y la razón de la diferencia se explica reemplazando el imán por un solenoide y observando la corriente.
Analícese la presencia de un conductor con corriente I próximo a una superficie que separa aire y hierro al considerarse el conductor imagen puede encontrarse la fuerza de atracción entre conductor y hierro.
Cuando en lugar de un semiespacio de hierro se tiene una chapa de cierto espesor se presentan reflexiones múltiples del conductor, y a cada imagen corresponde un factor.
También se produce este efecto cuando se tiene una capa de aire entre dos cuerpos (muy grandes) de hierro, las reflexiones múltiples en este caso como ya comentamos son totalmente análogas a observarse entre dos espejos paralelos, cada imagen con su correspondiente factor (signo y valor).
Para razonar obsérvese (Figura 945) que la superficie a crea la imagen b¢ de b y la a¢ ¢ de a¢ y así siguiendo.
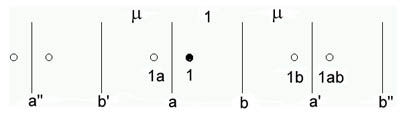
El conductor 1 tiene su imagen 1a debido a a y 1b debido a b.
La imagen de 1a debida a b aparece en 1ab, y sucesivamente otras imágenes.
Viendo esto en forma más simplificada (pero correcta) alrededor de cada imagen a se tienen el conductor 1 y su imagen 1a.
A cada imagen corresponde además un factor (Figura 946) que depende de la multiplicidad de la imagen y del área en la que se quiere estudiar el campo.
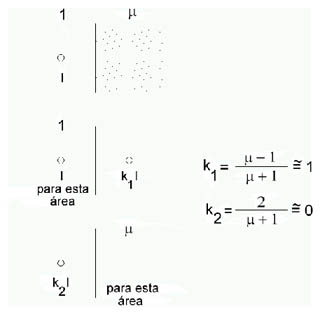
Al examinar la zona de aire (con permeabilidad 1), y supuesto m infinito k1 = 1, por lo que conductor e imágenes todos son con igual corriente (en el mismo sentido).
Se examinamos la zona de hierro se observa que se anulan las imágenes ya que k2 = 0.
Se propone analizar el problema de un conductor sumergido en una chapa de hierro para este caso las imágenes son las mismas pero los factores cambian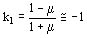 
y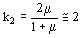 
.
Al examinar la zona de hierro algunas imágenes corresponden a corrientes de distinto sentido (Figura 947).
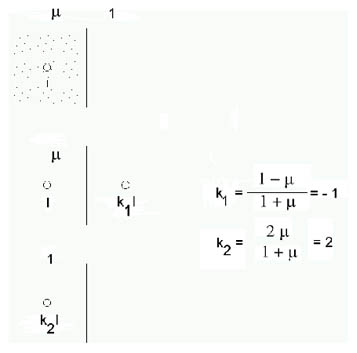
Al examinar la zona de aire el factor para la corriente en la chapa es 2.
2.6 LAS ECUACIONES DE MAXWELL
Los campos eléctricos y magnéticos cumplen las ecuaciones de Maxwell, que son simples de enunciar pero son bastante complejas de comprender, ellas relacionan magnitudes eléctricas y magnéticas.
A partir de la ley de Ampere:
A partir de la ley de Faraday:
A partir de la ley de Gauss:
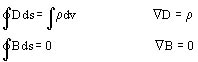
Hay además otras relaciones fundamentales, la ley de Ohm:
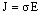
la relación de continuidad:
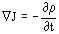
las relaciones de fuerzas:
F = Q E dF = I ´ B dl
las relaciones constituyentes:
D = e E = e0 E + P B = m H = m0 (H+M)
Estas relaciones se simplifican al aplicarlas al espacio libre de corriente y de densidad de carga J = 0 , r = 0.
En el estudio de las máquinas eléctricas se adoptan simplificaciones, las derivadas respecto al tiempo se consideran nulas, el campo entonces es electrostático, o magnetoestático.
BIBLIOGRAFIA
- John D. Kraus, Electromagnetismo (Mc Graw Hill).
- G. M. Pestarini, Elettromeccanica Volume I Fondamenti di costruzione comuni a tutte le macchine (Edizioni Italiane - Roma).
- Carrer, Note di Elettrotecnica (Levrotto e Bella - Torino).
- H. H. Skilling, Los fundamentos de las ondas eléctricas (Librería del Colegio).
- Andre Angot, Moderna matemática para ingenieros con especial aplicación para ingenieros electrotécnicos, electrónicos y físicos. (Librería y Editorial Nigar - Buenos Aires).
- Louis A. Pipes, Matemáticas aplicadas para ingenieros y físicos (Mc Graw Hill Book Co.).
- Ivan S. Sokolnikoff y Elizabeth S. Sokolnikoff, Matemática superior para ingenieros y físicos (Librería y Editorial Nigar - Buenos Aires).
- A. V. Netushil y K. M. Polivanov, Principios de Electrotecnia 3 - Teoría del campo electromagnético.
Copyright 2008 - 2012 INDUCOR INGENIERIA S.A. | Todos los derechos reservados | CCS | HTML