Advanced
Cable Testing
CALCULO Y DISEÑO DE MAQUINAS ELECTRICAS
APENDICE 10 - CORRIENTES DE VACIO Y DE INSERCION
La corriente de vacío
La corriente de vacío es un tema que los calculistas de la época clásica investigaron pero con éxito limitado. Se trata de un tema donde la alinealidad del hierro pone en crisis a quien con gran rapidez y firmeza resuelve los problemas lineales que son la mayoría de los que se encuentran en los cálculos de máquinas eléctricas.
Por otra parte a los fines del cálculo de la máquina la corriente de vacío es un parámetro que el proyectista cree bueno limitar, y para ello usa materiales mejores, y controla el corte de las chapas y armado del núcleo para reducir los entrehierros equivalentes, cuando en cambio no es necesaria la limitación, el proyectista acepta lo que le dará la máquina en ensayo, y si se le piden datos hablará con grosera aproximación.
Para quienes proyectan instalaciones que crecen más y más, la corriente de vacío y más aún la corriente de inserción de un transformador alcanzan en casos especiales una importancia tremendamente crítica, que ha impulsado el desarrollo de modelos para estudios transitorios.
La medición de la corriente
En el ensayo de vacío del transformador se mide la corriente con instrumentos de valor eficaz, y se obtiene una tabla que relaciona tensión de excitación y corriente de vacío en valores eficaces, pero si se registra la corriente, o se la observa con un osciloscopio, surge evidente la alinealidad y la medición prácticamente pierde significado.
La corriente de vacío se debe medir en los arrollamientos alimentados con la tensión y frecuencia nominales, para el tope principal o con la tensión del tope correspondiente si el ensayo está indicado para un tope distinto del nominal.
Los restantes arrollamientos deben estar abiertos, y si está previsto un arrollamiento en triángulo que debe funcionar abierto, es decir no cargable (por ejemplo para medición de la tensión homopolar), éste no debe cerrarse.
La fuente de alimentación de las tres columnas debe ser lo más posible simétrica y sinusoidal.
Para ello se debe medir la tensión con voltímetros que respondan al valor medio de la tensión aplicada (bobina móvil) con escala graduada en valor eficaz y simultáneamente en paralelo voltímetros que respondan al valor eficaz (electrodinámicos).
Cuando se ensayan transformadores trifásicos, la tensión medida es la de línea si el arrollamiento energizado está en triángulo, y entre bornes de fase y neutro si el arrollamiento energizado es YN o ZN.
La forma de onda de la tensión se considera satisfactoria (sinusoidal) si la diferencia de las lecturas entre los voltímetros de valor medio y valor eficaz no supera el 3% (es decir sí la tensión es suficientemente sinusoidal).
El programa ATP para resolver transitorios electromageticos
Desde hace largo tiempo el ATP nos ofrece la posibilidad de estudiar los fenómenos relacionados con las corrientes de vacío, inserción, y otros efectos que se presentan con transformadores, la dificultad se encuentra en obtener los datos representativos.
Si estos se obtienen de ensayos válidos o se logran estimar correctamente, armar el modelo para ATP es inmediato, el ATPDraw ha facilitado aún más este acercamiento permitiendo llegar también a aplicaciones didácticas.
La dificultad se mantiene en lograr una buena representatividad de los datos de las máquinas que se quieren investigar frente a un fenómeno que el ATP resuelve eficientemente.
El ATP es un programa con enormes posibilidades, que supera ampliamente los objetivos de este tratado orientado a las máquinas eléctricas.
Las facilidades asociadas al ATP permiten tomar casos de un ejemplo y utilizarlos como si se tratara de un programa especialmente desarrollado sólo para resolver dicho ejemplo.
En los ejemplos que contienen elementos conocidos es posible modificar sus parámetros (datos del programa) y ejecutar el ATP como si se tratara de un programa particular, que sólo resuelve el circuito que muestra el ATPDraw (preprocesador de datos).
Se obtiene de estas acciones los resultados de interés, quien es curioso comenzará a tratar de hacer más modificaciones, no sólo de parámetros sino también del circuito, queriendo aprender a usar el ATP, pero le recordamos que este no era el objetivo cuando inició el estudio de los temas de máquinas eléctricas.
Llegó la hora de responder otra pregunta que la hacen quienes piden al proyectista datos del transformador: corrientes de inserción, corrientes de vacío, ¿qué valores propone el calculista?
Pensamos avanzar por el camino más simple, disponemos de ATP, entonces es lógico durante el cálculo de la máquina, generar los datos que ATP requiere, con ellos preparar el modelo y realizar con ATP en cálculo de las corrientes de vacío y de inserción, y todas las simulaciones que utilizan el modelo de transformador que se propone.
La evaluación de la corriente
La necesidad de que el calculista de la máquina entregue algún dato que permita una evaluación de la corriente de vacío, que a máquina construida debe obtenerse en el ensayo, generó propuestas de fórmulas que permiten su determinación.
El programa TRADIM incorpora estas fórmulas obteniéndose más resultados de utilidad.
Pensemos en un transformador monofásico de columnas, aplicamos a un arrollamiento tensión de cierto valor eficaz, en el núcleo se presenta cierto flujo y cierta inducción correspondiente, a su vez aparece cierto campo magnético relacionado con la corriente en la bobina.
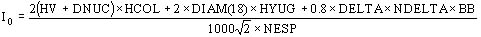
Se observan las longitudes de los caminos magnéticos en las columnas (HV+DNUC) y en el yugo DIAM(18), y los campos HCOL y HYUG obtenidos a partir de la inducción BB.
El entrehierro DELTA que en construcciones bien hechas puede adoptarse igual a 0.035 mm, y el número de entrehierros NDELTA que el proyectista está obligado a mantener limitado pero permitiendo la construcción de la máquina, completan los datos indispensables para esta evaluación.
El número de espiras NESP debe indicarse para la tensión nominal, como el programa determina esta valor para la tensión máxima, es necesario corrigirlo con la relación UC / UM.
Para los distintos tipos de núcleos de columnas (3 o 5), o acorazados, estas fórmulas cambian pero no en su esencia conceptual.
El caso particular, y quizás el más frecuente, de transformadores trifásicos de tres columnas presenta una asimetría constructiva causa de que se observe al medir que de las tres corrientes de vacío de las tres fases, una (la fase central) sea distinta, a los fines del cálculo el factor 2/3 trata de promediar y proponer un único valor para no dificultar el modelo que después se desarrollará.
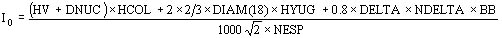
En los transformadores acorazados el flujo en los yugos se divide mitad en cada lado, y luego a las columnas externas, que son de sección mitad de la interna.
Para distintos valores de la tensión de excitación aplicada se obtiene la inducción BB y la corriente de vacío, lo que permite construir una tabla de valores entre los límites de interés.
Con el programa se desarrollan los cálculos incluyendo estos conceptos, y con los resultados es construible el modelo de transformador para el estudio de transitorios.
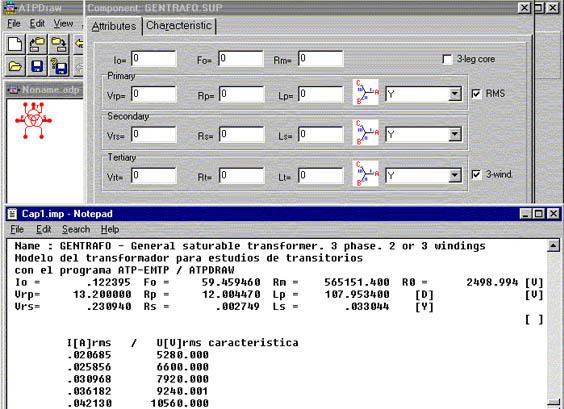
La disponibilidad del programa ATP, y las facilidades que presenta el ATPDraw para la carga de datos, y su aplicación didáctica, nos impulsó a presentar la salida de TRADIM en forma similar a como ATPDraw los presenta (ver cuadro 1), para construir el modelo y entonces facilitar las verificaciones posibles del transformador calculado, en el poderoso ambiente ATP.
La carga del modelo
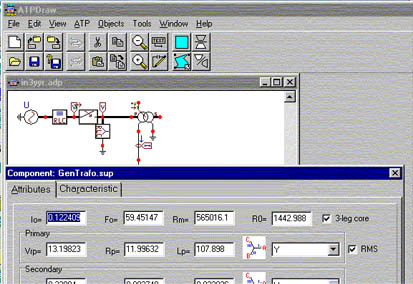
Se observan en el cuadro 1, superpuestas las pantallas de ATPDraw, la hoja donde se construye el modelo gráfico de la red a estudiar, la planilla GENTRAFO.SUP/Attributes donde se vuelcan los datos del modelo de transformador, y en el Notepad la salida del cálculo del transformador obtenida ejecutando TRADIM, y cuyos valores deben ser copiados en las planillas de ATPDraw.
La salida del programa TRADIM incluye además I[A]rms / U[V]rms, que son los datos útiles para ATP, en efecto la planilla GENTRAFO.SUP contiene una segunda página "Characteristics" en la que se vuelcan las características magnéticas (saturación) del transformador.
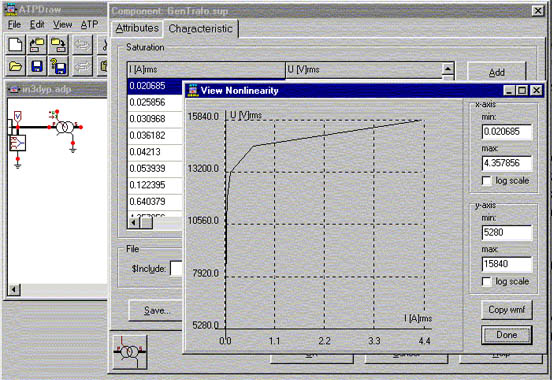
Es bueno verificar que las características calculadas por TRADIM incluyan el codo de saturación ya que la buena representación de éste es importante para los cálculos que realiza ATP (ver cuadro 2), ATPDraw muestra esta característica en el gráfico que se pide desde GENTRAFO.SUP/ Characteristics (pudiendo verse con escalas lineales o logarítmicas).
Las características de excitación en Arms/m disponibles para laminación de grano orientado están dadas normalmente hasta valores de inducción de 1.9 T (lo usual en el cálculo del transformador para la condición nominal de funcionamiento es no exceder 1.8 T), para el cálculo de la corriente magnetizante se requiere superar el valor de 2 T.
El ATP utiliza un modelo circuital que se observa en la figura 646, el transformador trifásico se forma con tres de estos módulos, adecuadamente conectados entre si en el primario y el secundario.
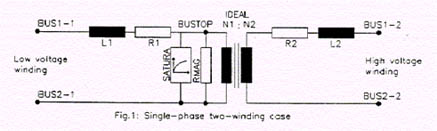
Completados los datos del transformador debe armarse dentro de ATP el circuito completo para el ensayo que se desea simular, la corriente permanente de vacío es un caso, la otra posibilidad es alimentando con una fuente con potencia de cortocircuito, determinar la corriente transitoria de inserción, también se puede someter el transformador a un cortocircuito encontrándose previamente en vacío o desconectado o cualquier otro transitorio que tenga sentido.
El producto del programa
El informe que el programa TRADIM desarrolla incluye gran cantidad de datos dimensionales y parámetros que se van determinando paso a paso, pensando en la aplicación didáctica creímos conveniente reunir todos los valores para generar el modelo de transformador como ATPDraw lo requiere.
Hasta ahora nunca nos fue fácil obtener del fabricante del transformador los datos que ATP necesita, es más sorprende constatar que algunos proyectistas desconocen la herramienta, que les permitiría avanzar y ayudar a quien quiere profundizar el comportamiento del transformador en la instalación.
La idea de agregar un módulo al programa TRADIM, que prepara datos para ATP parece ser la más adecuada, se amplía así la posibilidad que el programa brinda, no sólo al alumno que se interesa de la construcción de las máquinas eléctricas, sino también satisface a quien quiere ponerlas a prueba dentro de un proyecto.
Los resultados de TRADIM reelaborados con el módulo agregado completan la planilla que sirve para cargar frente al ATPDraw los datos del modelo. Expliquemos lo que se hace en el módulo final de TRADIM para preparar estos valores.
El módulo donde se desarrollan todas las tareas es GENTRA, y este además de hacer tareas menores llama sucesivamente las siguientes rutinas: TRAINS, ENTREH, CORVAC, TRAFO3, TRAFO1.
Examinemos lo que se hace en detalle, previamente se han ingresado datos y el programa de cálculo ha determinado valores de interés que están disponibles para la rutina GENTRA.
Son todavía necesarios algunos datos más:
- DELTA - entrehierro equivalente (mm)
- NDELTA - cantidad de entrehierros por fase
- ATP - arrollamiento desde el que se excita la máquina
- X0 - reactancia de secuencia cero en (pu)
- BREL - inducción residual (pu)
Como se ha hecho para todo el programa frente a datos nulos se fijan valores adecuados, si ATP = 0 el programa elige el arrollamiento de mayor tensión para excitarlo.
La primera rutina TRAINS determina un valor de la corriente de inserción en modo aproximado con la finalidad de tener el valor disponible como primera respuesta.
Siendo datos:
- B - inducción máxima (T)
- BR - inducción residual (T)
- SN - sección núcleo de hierro (m²)
- HB - altura del bobinado (m)
- NESP - número de espiras del arrollamiento insertado
- DIAMI - diámetro interno arrollamiento insertado (m)
- ESPARR - espesor arrollamiento (m)
Resultados:
- Sección interna del arrollamiento (m²)
- corriente de pico (
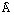) con inducción residual - corriente de pico (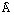) sin inducción residual
- relación corrientes de pico
- IPIC / IPB0
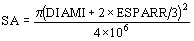
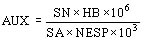
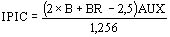
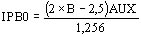
El valor de la corriente de inserción así calculada no depende del conexionado del transformador, al poner a prueba el modelo, simulando la inserción observaremos la dependencia del conexionado D o Y de la vinculación de los flujos homopolares, y de la existencia de otros arrollamientos en D, perfeccionando así la primera estimación.
TRAINS en sus fórmulas tiene en cuenta la inducción residual, esto también es posible con ATP pero complicando el modelo, y este tema queda para más adelante.
Sigue la rutina ENTREH que selecciona valores adecuados de DELTA y NDELTA cuando no se han fijado en los datos de la corrida. La tabla básica es:
| Tabla I | Trifásico columnas | Trifásico acorazado | Trifásico cinco col. | Monofásico columnas | Monofásico acorazado |
| KFAS | 3 | 3 | 3 | 1 | 1 |
| NUCLEO | 1 | 3 | 5 | 1 | 3 |
| DELTA | 0.035 | 0.035 | 0.035 | 0.035 | 0.035 |
| NDELTA | 2 | 4 | 2 | 4 | 4 |
La rutina CORVAC calcula la corriente de vacío en las condiciones que se fijan, en esta primera vez se la usa para las condiciones nominales.
Esta rutina usa también fórmulas simples que proponen determinar la corriente de excitación de la columna en base a la tensión de excitación presente.
Con la inducción BB en la columna se determina el campo HCOL, con la relación CYUGO se determina la inducción en el yugo BBY y el campo HYUG.
Se conoce la característica del hierro B-AS/M mediante varios puntos, y los valores de campo se obtienen por interpolación.
Con los valores de inducción y campo se determina la corriente magnetizante, que depende del tipo de transformador.
Durante el desarrollo de esta parte, se presentaron algunas dificultades que es bueno señalar, se debe tener en cuenta que los puntos de la representación de la característica del hierro deben superar suficientemente la condición nominal, y que los gráficos de la característica son logarítmicos en un eje y lineales en el otro, por lo que una simple interpolación o extrapolación lineal no es lo más adecuado, especialmente cuando el punto buscado sale del rango de datos, debe entonces desarrollarse una interpolación o extrapolación logarítmica, o buscar otra forma de interpolación o extrapolación más precisa.
Según el tipo de núcleo que se utilice el flujo puede dividirse mitad a cada lado, o mantenerse único, por otro lado puede encontrar un camino una única vez o encontrarlo dos veces.
Los transformadores de 3 y 5 columnas tienen corrientes magnetizantes de las columnas laterales distintas de la central, pero en la representación se toma un promedio ponderado, se tienen así algunos factores F2 y F23.
| Tabla II | Trifásico columnas | Trifásico acorazado | Trifásico cinco col. | Monofásico columnas | Monofásico acorazado |
| F2 | 1 | 2 | 1 | 2 | 2 |
| F23 | 2 / 3 | 1 | 2 / 3 | 1 | 1 |
Se calculan entonces:
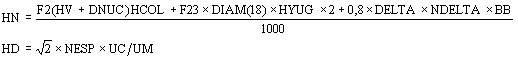
El número de espiras debe indicarse para la tensión nominal, como el programa determina este valor para la tensión máxima, es necesario corrigirlo con la relación UC / UM.
- La corriente magnetizante (A)
- La corriente de pérdidas (A)
- Lla corriente de vacío (A)
- La rutina TRAFO3 presenta los valores para el modelo ATP del transformador trifasico (2 o 3 arrollamientos).
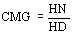
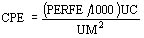
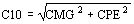
Se determina la resistencia de pérdidas:
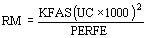
(ohm)
Al hacer esto se supone que RM es constante, independiente de UC lo cual no es tan cierto, pero la corrección no es importante para este trabajo.
El flujo WB1 (finalmente adoptado por el programa una vez encontrada una solución constructiva del devanado interno), también debe referirse a la tensión nominal, como se ha comentado antes se corrige con el número de espiras.
Los transformadores del tipo de tres columnas (a flujos vinculados) tienen una impedancia a la secuencia cero que no es igual a la directa, el ATP los llama 3-leg core-type, y se debe determinar el valor de reluctancia de secuencia cero del camino de retorno en aire.
Esta determinación se hace a partir de X0, dado como dato en pu, en general se puede estimar este valor como 1.
La impedancia base es:
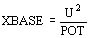
La inductancia homopolar resulta:
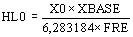(H)
Expresándola en (mH)
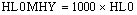
La reluctancia finalmente es:
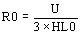
Si el núcleo no es de columnas los valores X0 y R0 no son de interés.
Luego se determina la resistencia del arrollamiento para el tope nominal:
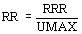
La reactancia se divide en dos partes en los transformadores de 2 arrollamientos (mitad cada parte) en los de tres se trabaja con la estrella equivalente, y para cada arrollamiento se repite esta tarea:
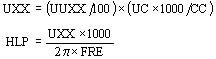
La rutina TRAFO1 realiza las mismas tareas para el transformador monofásico.
Por último se calculan e imprimen varios pares de valores: corriente de excitación (en valor eficaz) determinada por CORVAC, tensión de excitación variable desde alrededor del 40% de la tensión nominal hasta el 130% de la misma.
Presentación de resultados, corriente de vacio
Los ejemplos que siguen en los que se hacen estos análisis, se han desarrollado con el programa ATP, (Alternative Transients Program, GNU Linux or DOS. All rights reserved by Can/Am user group of Portland, Oregon, USA. Source code date is 26 September 2001).
Observaremos primero la corriente magnetizante en régimen permanente de un transformador trifásico de 315 kVA, considerando distintos casos de conexión en alta tensión y en baja tensión, Y o D, con y sin el neutro a tierra, y situaciones con flujos vinculados (transformador trifásico de tres columnas) o no vinculados (núcleo acorazado o tres transformadores monofásicos).
Las formas de la onda de corriente magnetizante son distintas según el caso que se analice, comenzaremos por las formas más simples de explicar, para llegar a los casos más complicados.
Para que las corrientes magnetizantes de las columnas sean las mismas, las tensiones aplicadas a las columnas se han hecho iguales en todos los transformadores, es decir, aquellos con arrollamiento en Y se alimentan con 13.2´ Ö 3 kV y los que tienen arrollamiento en D con 13.2 kV, con corrientes nominales respectivamente de 7.95 A (para Y) y 13.78 A (para D), en ambos casos la misma corriente en la columna de 7.95 A.
Se desarrollan los siguientes casos:
| Tabla III | Arr. 1 | Neutro | Arr. 2 | Flujos | Lotes datos | Figura |
| 1 | YN | Tierra | Y | No vinculados | In3yyp.adp |  |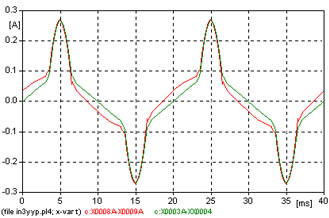
| 2 | Y | Aislado | Y | No vinculados | In3yyq.adp |  |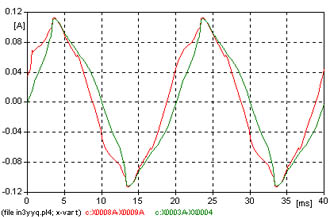
| 3 | YN | Tierra | Y | Vinculados | In3yyr.adp |  |
| 4 | Y | Aislado | Y | Vinculados | In3yys.adp |  |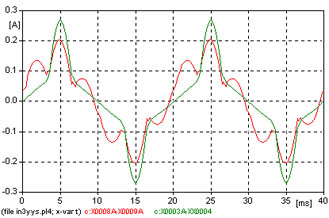
| 5 | YN | Tierra | D | No vinculados | In3ydp.adp |  |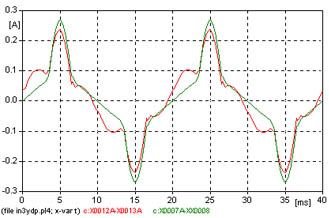
| 6 | Y | Aislado | D | No vinculados | In3ydq.adp |  |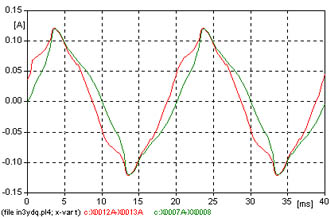
| 7 | YN | Tierra | D | Vinculados | In3ydr.adp |  |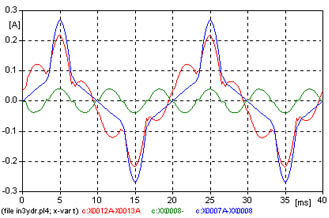
| 8 | Y | Aislado | D | Vinculados | In3yds.adp |  |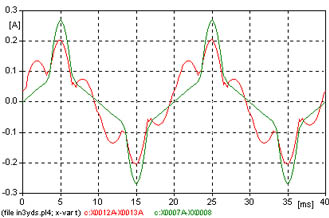
| 9 | D | Aislado | Y | No vinculados | In3dyp.adp |  |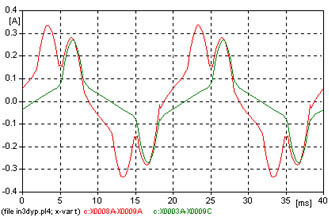
| 10 | D | Aislado | Y | Vinculados | In3dyr.adp | |
| 11 | D | Aislado | D | No vinculados | In3ddq.adp | |
| 12 | D | Aislado | D | Vinculados | In3dds.adp |
1 - Transformador YN y neutro del lado de alta tensión a tierra, sin vinculación de flujos de columnas (como si se tratara de 3 transformadores monofásicos o un trifásico acorazado o de cinco columnas).
La excitación de la columna es sinusoidal, para la característica de saturación del hierro la forma de la corriente puede verse en la figura 613. Se observa la corriente magnetizante y la corriente de vacío (que incluye las pérdidas).
Los resultados del análisis de Fourier, de la corriente de vacío, se observan en la figura 622, se notan armónicas 3, 5 y 7 de amplitud importante, pudiendo determinarse el valor eficaz total que se puede comparar con el valor de pico (ver nuevamente la figura 613 notándose 0.270 Apico)
| Harm. | Amplitud (Arms) | Amplitud (%) |
| 1 | 0.1116 | 100 |
| 3 | 0.0453 | 40.65 |
| 5 | 0.0283 | 25.43 |
| 7 | 0.0122 | 10.96 |
| THD | 49.436 % | |
| Eficaz | 0.1243 |
Una observación interesante es la corriente de neutro que muestra sólo (prácticamente) tercera armónica (homopolar), cuyo valor eficaz alcanza 0.1367 Arms con pico de 0.1933 A.
2 - Comparemos la corriente del caso anterior con la que se obtiene al tener el neutro de alta tensión aislado de tierra (Y y), y manteniendo las columnas sin vinculación de flujos.
Siendo flotante el centro estrella, la tensión aplicada a la columna ya no es sinusoidal, la corriente obtenida se observa en la figura 614, y el análisis de Fourier de la figura 623 no muestra tercera armónica, sólo armónicas 5 y 7 menores que en el caso de la figura 622.
| Harm. | Amplitud (Arms) | Amplitud (%) |
| 1 | 0.0716 | 100 |
| 5 | 0.00422 | 5.89 |
| 7 | 0.00282 | 3.93 |
| THD | 7.2354 % | |
| Eficaz | 0.0718 |
La figura 647 muestra la tensión aplicada a una fase, y la tensión relevada en el neutro con una importante componente de tercera armónica, también se ve la diferencia entre ambas tensiones, de característica forma triangular.
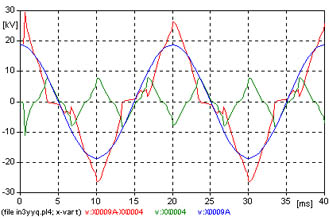
3 - Transformador YN y neutro de alta tensión a tierra, con vinculación de flujos de las tres columnas.
La corriente de vacío se ve en la figura 615, la excitación de la columna es sinusoidal, se observa la corriente magnetizante y la corriente de vacío.
Los resultados del análisis de Fourier, de la corriente de vacío, se observan en la figura 624, y la tabla que debe compararse con los otros casos.
| Harm. | Amplitud (Arms) | Amplitud (%) |
| 1 | 0.1115 | 100. |
| 3 | 0.0115 | 10.31 |
| 5 | 0.0287 | 25.73 |
| 7 | 0.0120 | 10.76 |
| THD | 30.091 % | |
| Eficaz | 0.1163 |
La corriente de neutro muestra sólo (prácticamente) tercera armónica (homopolar), con valor eficaz 0.0351 Arms y pico de 0.0504 A.
La curiosidad de entender la diferencia de este caso con los anteriores pregunta como ha cambiado el circuito, véase la figura 648, en el que todavía faltan las conexiones entre los arrollamientos que se deben adecuar a cada caso.
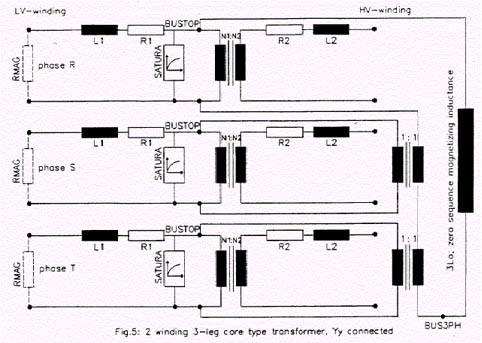
Respecto de la figura 646, ha aparecido la inductancia 3 ´ L0, que acopla (con transformadores adicionales) los tres módulos de transformador monofásico, y que en el modelo ingresa con el valor R0 que corresponde llenar cuando se tilda 3 leg core, ver cuadro 3.
4 - Comparemos la corriente del caso anterior con la que se obtiene al tener el neutro de alta tensión aislado de tierra (Y y), con vinculación de flujos.
La figura 616 muestra la corriente de vacío, el análisis de Fourier muestra diferencias con el caso anterior figura 625.
| Harm. | Amplitud (Arms) | Amplitud (%) |
| 1 | 0.1117 | 100 |
| 5 | 0.0288 | 25.783 |
| 7 | 0.0119 | 10.65 |
| THD | 28.253 % | |
| Eficaz | 0.116 |
Al no haber neutro, no hay corrientes homopolares, no hay tercera armónica, y al estar los flujos vinculados, la tensión relevada en el neutro es muy pequeña.
5 - Transformador YN d con neutro a tierra, y sin vinculación de flujos de columnas (como si se tratara de 3 transformadores monofásicos o un trifásico acorazado o uno de cinco columnas).
Si se observa figura 617 que muestra la corriente de vacío, se nota similitud con los casos en que los flujos están vinculados, en efecto el arrollamiento d cumple esa función.
Los resultados del análisis de Fourier, de la corriente de vacío, se observan en la figura 626, para las armónicas se obtienen los valores siguentes:
| Harm. | Amplitud (Arms) | Amplitud (%) |
| 1 | 0.1115 | 100 |
| 3 | 0.0217 | 19.46 |
| 5 | 0.0286 | 25.65 |
| 7 | 0.0121 | 10.85 |
| THD | 34.291 % | |
| Eficaz | 0.1178 |
La corriente de neutro figura 649, muestra sólo (prácticamente) tercera armónica (homopolar), cuyo valor eficaz alcanza 0.658 Arms con pico de 0.946 A.
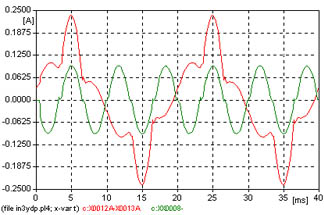
6 - Transformador Y d con neutros aislados, sin vinculación de flujos de las tres columnas.
La corriente de vacío se ve en la figura 618, la excitación de la columna es sinusoidal, se observa la corriente magnetizante y la corriente de vacío.
Los resultados del análisis de Fourier, de la corriente de vacío, se observan en la figura 627, y los valores de la tabla que sigue deben compararse con los otros casos.
| Harm. | Amplitud (Arms) | Amplitud (%) |
| 1 | 0.0751 | 100. |
| 5 | 0.0053 | 7.057 |
| 7 | 0.0033 | 4.394 |
| THD | 8.6808 % | |
| Eficaz | 0.0754 |
La figura 650 muestra la tensión aplicada a una fase, y la tensión relevada en el neutro y la diferencia entre ambas tensiones, de característica forma triangular.
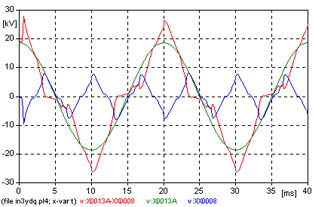
7 - Transformador YN d con neutro a tierra, con vinculación de flujos de las tres columnas.
En la figura 619, se observa la corriente de vacío, la magnetizante, la corriente de neutro.
Los resultados del análisis de Fourier, de la corriente de vacío, se observan en la figura 628, y en la tabla cuyos valores deben compararse con los otros casos.
| Harm. | Amplitud (Arms) | Amplitud (%) |
| 1 | 0.1115 | 100. |
| 3 | 0.00897 | 8.0448 |
| 5 | 0.0292 | 26.1883 |
| 7 | 0.0120 | 10.7623 |
| THD | 29.405 % | |
| Eficaz | 0.1162 |
La corriente de neutro muestra sólo (prácticamente) tercera armónica (homopolar) valor eficaz 0.0275 A, pico 0.0396 A.
8 - Comparemos la corriente del caso anterior con la que se obtiene al tener el neutro de alta tensión aislado de tierra (Y d), con vinculación de flujos.
La figura 620 muestra la corriente de vacío, el análisis de Fourier se observa en la figura 629.
| Harm. | Amplitud (Arms) | Amplitud (%) |
| 1 | 0.1117 | 100. |
| 5 | 0.02887 | 25.8460 |
| 7 | 0.01196 | 10.7073 |
| THD | 28.265 % | |
| Eficaz | 0.1160 |
Al estar los flujos vinculados la tensión relevada en el neutro es pequeña.
9 - Transformador D y, sin vinculación de flujos de columnas (como si se tratara de 3 transformadores monofásicos o un trifásico acorazado o uno de cinco columnas).
La figura 621 muestra la corriente de vacío, el análisis de Fourier se observa en la figura 630 y en la tabla.
| Harm. | Amplitud (Arms) | Amplitud (%) |
| 1 | 0.1929 | 100. |
| 5 | 0.0492 | 25.505 |
| 7 | 0.0211 | 10.938 |
| THD | 28.036 % | |
| Eficaz | 0.2002 |
En la corriente de vacío se observan dos picos, que se justifican por la conexión D del arrollamiento que presenta dos ramas del transformador en cada línea, observándose sucesivamente el pico que corresponde a una rama, y el de la otra. Esta forma de la corriente es muy distinta de las que se han obtenido con conexiones Y, que mostraban sólo un pico, eventualmente con dos pequeños picos laterales.
10 - Transformador D y, con vinculación de flujos de columnas (como si se tratara de un trifásico de tres columnas).
11 - Transformador D d, sin vinculación de flujos de columnas (como si se tratara de 3 transformadores monofásicos o un trifásico acorazado o uno de cinco columnas).
12 - Transformador D d, con vinculación de flujos de columnas (como si se tratara de un trifásico de tres columnas).
Estos tres últimos casos presentan una corriente igual a la del caso 9, por lo que se cita la figura 621, es decir con lado excitación conectado en D la corriente de vacío es independiente de la vinculación de flujos, al menos con la magnitud de los parámetros con que se trabaja, y de la conexión de los secundarios y o d.
| Tabla IV | Conexión | Flujos | 1 | 3 | 5 | 7 | Eficaz | Figura |
| 1 | YN/y | NV | 0.1116 | 0.0453 | 0.0283 | 0.0122 | 0.1243 |  |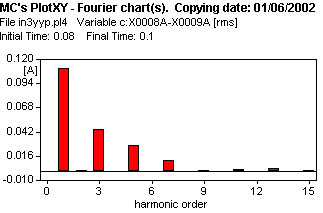
| 2 | Y/y | NV | 0.0716 | - | 0.0042 | 0.0028 | 0.0718 |  |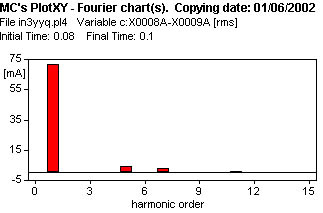
| 3 | YN/y | V | 0.1115 | 0.0115 | 0.0287 | 0.0120 | 0.1163 |  |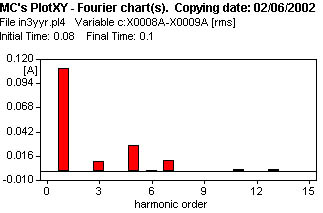
| 4 | Y/y | V | 0.1117 | - | 0.0288 | 0.0119 | 0.1160 |  |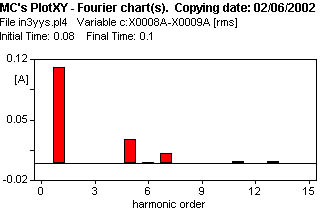
| 5 | YN/d | NV | 0.1115 | 0.0217 | 0.0286 | 0.0121 | 0.1178 |  |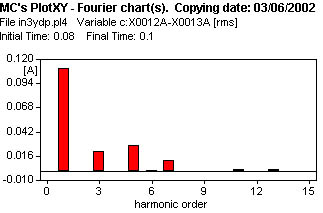
| 6 | Y/d | NV | 0.0751 | - | 0.0053 | 0.0033 | 0.0754 |  |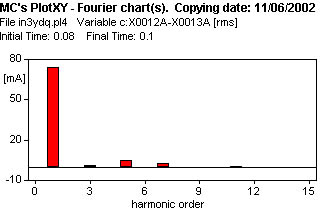
| 7 | YN/d | V | 0.1115 | 0.00897 | 0.0292 | 0.0120 | 0.1162 |  |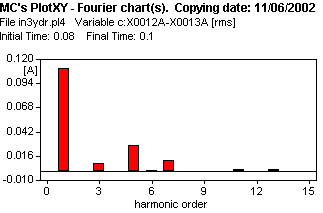
| 8 | Y/d | V | 0.1117 | - | 0.0289 | 0.0119 | 0.1160 |  |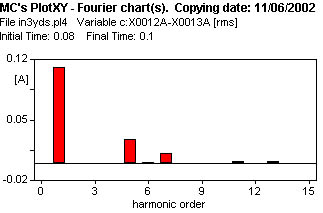
| 9 | D/y | NV | 0.1929 | - | 0.0492 | 0.0211 | 0.2002 |  |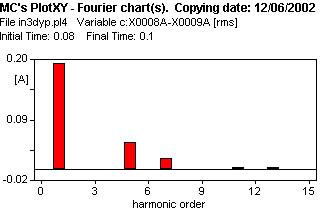
| 10 | D/y | V | - | |||||
| 11 | D/d | NV | - | |||||
| 12 | D/d | V | - |
Corriente de inserción
En ausencia de magnetización residual del núcleo, si la inserción se efectúa cuando la tensión pasa por el valor máximo, el flujo desfasado 90° en atraso debe valer cero, en consecuencia la magnetización se realiza regularmente (a partir de flujo cero) y el transitorio no se manifiesta.
En la práctica no es posible controlar el instante de inserción. Para sistemas trifásicos la condición de que la tensión pase por el valor máximo podría solamente lograrse para una de las fases.
Además, la magnetización residual del núcleo está siempre más o menos presente.
En consecuencia el fenómeno del pico de corriente durante la inserción en la práctica no puede evitarse.
El valor Br de la inducción residual puede alcanzar aproximadamente al 94% del valor de pico. Este valor depende de la forma del ciclo de histéresis (material utilizado), de la frecuencia y de la inducción máxima considerada.
No depende del instante en el cual los contactos del interruptor se separan, la extinción de la corriente se produce en correspondencia con su pasaje por cero.
El valor de la inducción residual puede verse influenciado por la presencia de una carga en bornes del transformador en el momento de la desconexión.
Una carga capacitiva importante, anticipando el pasaje por cero de la corriente, puede reducir el valor de la inducción residual (una oscilación amortiguada entre la inductancia del transformador y la carga capacitiva, tiende a desmagnetizar el núcleo).
La peor situación, desde el punto de vista del pico de corriente, se tiene cuando el transformador es desconectado en vacío.
En la figura 651 se analiza este caso, observándose que en el instante 1 se produce la desconexión, y la inducción del núcleo permanece al valor residual +Br.
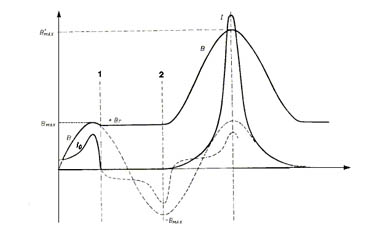
Supongamos ahora que el transformador se reconecta en el instante 2, cuando la tensión (no representada) pasa por el valor cero; se observa que si el transformador hubiese permanecido conectado la inducción hubiese tenido el valor máximo negativo -Bmax (ver figura 651).
La inducción describe una onda sinusoidal de amplitud similar a la onda sinusoidal en estado de régimen, pero que parte del valor residual +Br.
Se hace notar que la corriente de vacío en estado de régimen I0 y el pico de corriente alcanzado durante la inserción no están en escala (este último puede alcanzar valores del orden de algún centenar de veces el primero).
Si se desprecian los elementos disipativos del circuito, y la eventual caída de la tensión de alimentación provocada por la corriente de inserción, los valores de inducción que se alcanzan superan los utilizados para el diseño de los transformadores, superando ampliamente los límites de saturación del núcleo.
Se puede determinar el valor de pico de la corriente de inserción con la expresión:
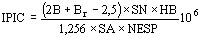
donde:
- B: inducción nominal en la columna (T)
- Br: inducción residual del núcleo (T)
- SN: sección neta columna (m²)
- HB: altura del bobinado (m)
- sección interna del arrollamiento alimentado (m²)
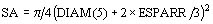
- NESP: espiras del arrollamiento alimentado (para tensión nominal)
La fórmula obtenida da el valor de cresta del primer pico de la corriente de inserción, es aproximada, tanto por la dificultad de valorar exactamente las condiciones de partida del transitorio (valor de la inducción residual del núcleo), como así también por las simplificaciones realizadas en la determinación de la inductancia del arrollamiento alimentado.
El arrollamiento de un transformador puede considerarse desde el punto de vista de los fenómenos de la inserción como un circuito compuesto por resistencia e inductancia en serie, el amortiguamiento del transitorio es proporcional a la relación R/L del circuito.
La inductancia del arrollamiento alimentado del transformador, a causa de la saturación del núcleo, varía continuamente durante un período y por lo tanto el valor del amortiguamiento.
La permeabilidad relativa del núcleo pasa de un valor próximo a 20000 para bajas inducciones a valores próximos a la unidad en condiciones de fuerte saturación. La relación R/L es en consecuencia muy grande en los primeros ciclos a partir de la inserción (núcleo sobresaturado), y se reduce a medida que la inducción del núcleo se aproxima a las condiciones normales de funcionamiento. Esto explica el rápido amortiguamiento de la corriente en los primeros períodos, y la más lenta extinción del transitorio de inserción, que puede demorar algunos segundos antes de que la corriente alcance el valor de vacío permanente.
En un circuito trifásico las corrientes de cada fase son independientes sólo si el arrollamiento alimentado está conectado en triángulo, o en estrella con el neutro conectado al neutro de la alimentación (con conductores o a través de la tierra).
Si el arrollamiento alimentado está conectado en triángulo, falta por lo tanto el aporte de las otras fases en la combinación de las corrientes de fase, para tener las corrientes de línea. Esto significa que si el pico de corriente de fase es n veces la corriente de fase de plena carga, en comparación con la corriente de línea el pico es solamente n/Ö 3 veces.
Si el arrollamiento alimentado está conectado en estrella sin neutro, o con el neutro no conectado al neutro de la alimentación, el comportamiento de la inserción es distinto, según que el transformador tenga o no otro arrollamiento en triángulo.
Si no tiene arrollamientos en triángulo, el potencial del neutro se desplaza, desequilibrando la estrella de tensión de fase de manera que se cumpla que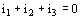 
, consecuentemente se tiene una reducción de la corriente de inserción.
Si en cambio se tiene un arrollamiento conectado en triángulo, la distribución de la corrientes es la indicada en la figura 652, una rama presenta doble corriente que las otras dos.
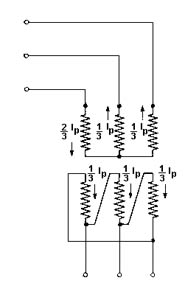
Presentación de resultados de inserción
Desarrollaremos en forma sistemática las inserciones de los distintos casos (que muestren interés) ya analizados para la corriente de vacío.
Recordemos que los transformadores con arrollamiento en Y se alimentan con 13.2´ Ö 3 kV y los D con 13.2 kV, en ambos casos presentan la misma corriente en la columna.
| Tabla V | Conexión | Flujos | Pico A | Lotes datos | Figuras | ||
| 1 s | 0 a 0.1 s | 0.9 a 1 s | |||||
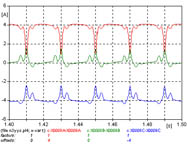
| 1 | YN/y | No Vinculados | 70.56 | n3yyp.adp |  |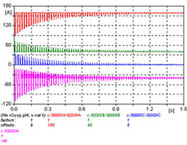
 |
 |
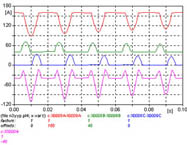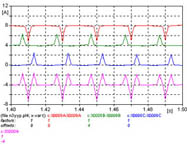| 2 | Y/y | NV | 42.07 | n3yyq.adp |  |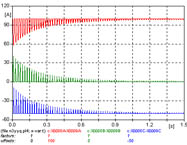
 |
 |
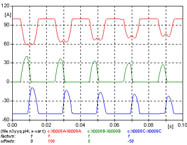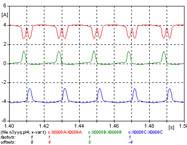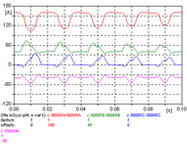
| 3 | YN/y | Vinculados | 55.00 | n3yyr.adp |  |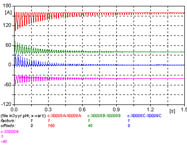
 |
 |
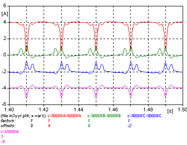| 4 | Y/y | V | 49.14 | n3yys.adp |  |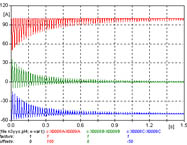
 |
 |
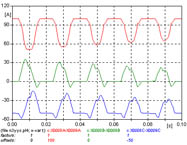| 5 | YN/d | NV | 60.08 | n3ydp.adp |  |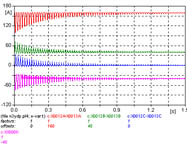
||
| 6 | Y/d | NV | 49.09 | n3ydq.adp |  |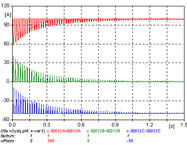
||
| 7 | YN/d | V | 54.02 | n3ydr.adp | |||
| 8 | Y/d | V | 49.38 | n3yds.adp | |||
| 9 | D/y | NV | 99.24 | n3dyp.adp |  |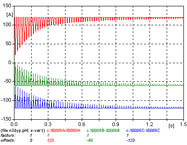
||
| 10 | D/y | V | 88.65 | n3dyr.adp | |||
| 11 | D/d | NV | 99.29 | n3ddq.adp | |||
| 12 | D/d | V | 99.24 | n3dds.adp | |||
1 - La corriente de inserción presenta el pico máximo en una fase. El pico inicial es elevado, casi 10 veces el valor eficaz de la corriente nominal, la amplitud de la corriente de inserción se reduce al 10% en menos de 1 segundo, características que se mantienen en todos los casos. Obsérvese el oscilograma de 1 segundo, y los detalles de los primeros 100 ms y últimos 100 ms del período simulado.
La figura 631 muestra las corrientes de las tres fases, y la corriente de neutro a tierra, la figura 632 muestra los primeros 100 ms, y la figura 633 muestra los últimos 100 ms de la simulación realizada.
2 - El pico máximo se presenta en las tres fases, prácticamente la misma amplitud. Se nota durante todo el transitorio que la corriente de la fase 1 se divide entre las fases 2 y 3.
La figura 634 muestra las corrientes de las tres fases, la figura 635 muestra los primeros 100 ms pudiendo verse el detalle de los primeros ciclos, y la figura 636 muestra los últimos 100 ms de la simulación realizada.
3 - El pico máximo se presenta en una fase, en las otras dos se presentan picos iguales ente si, de menor valor, la corriente de neutro es aún de menor amplitud, poniendo en evidencia la influencia de que los flujos estén vinculados.
La figura 637 muestra las corrientes de las tres fases, la figura 638 muestra los primeros 100 ms pudiendo verse el detalle de los primeros ciclos, y la figura 639 muestra los últimos 100 ms.
4 - Similar al caso 3, pero sin neutro, los valores de pico son ligeramente menores. La figura 640 muestra las corrientes de las tres fases, la figura 641 muestra los primeros 100 ms y la figura 642 muestra los últimos 100 ms.
5 - Merece los mismos comentarios que el caso 1, aunque los valores alcanzados son inferiores. La figura 643 muestra las corrientes de las tres fases, y la de neutro.
6 - Análogo al caso 2, pero los valores pico alcanzados son superiores. La figura 644 muestra las corrientes de las tres fases.
7 - Es muy similar al 3, y el caso 8 es al 4.
9 - Se inicia la serie de transformadores con lado excitación en conexión D. La figura 645 muestra las corrientes de las tres fases.
10 - Presenta un pico ligeramente inferior, el caso 11 en cambio presenta un pico que supera ligeramente al caso 9, y el caso 12 presenta igual valor que el caso 9.
Inserción de un segundo transformador
La red representada tiene bajo nivel de cortocircuito (50 MVA), en ella hay un transformador (315 kVA Dy) conectado y se inserta un segundo transformador igual, se observa en la figura 653 que en correspondencia con la corriente de inserción del segundo transformador, la corriente de vacío del primer transformador se incrementa, nótese que se ha multiplicado por un factor 10 para apreciar el fenómeno.
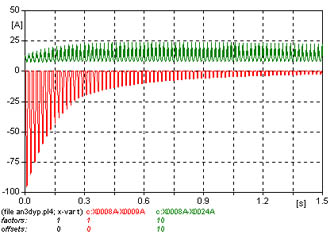
Lentamente la corriente de vacío del primer transformador se incrementa, la figura 654 muestra los primeros instantes, y la figura 655 muestra el final de la simulación, se aprecia que el transitorio tiene una gran duración.
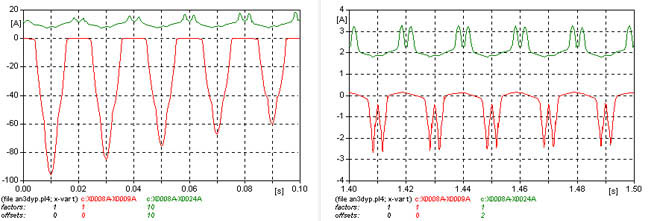
Inserción de un transformador con carga reactiva
Se inserta un transformador (315 kVA Dy) alimentado desde una red de 500 MVA y con una carga secundaria puramente reactiva, que absorbe en régimen la corriente nominal, obsérvese en la figura 656 la corriente de inserción y carga, el pico inicial alcanza 127.9 A que debe compararse con la inserción del caso 9 que en vacío alcanzó 99.24 A de pico.
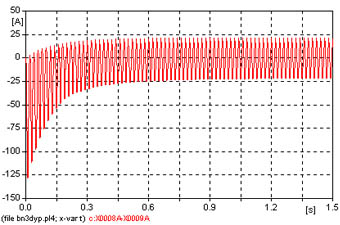
Al establecerse la corriente como se observa en la figura 657 se nota cierta deformación, al final da la simulación si bien la corriente ya casi es simétrica todavía se observa deformación en una de las semiondas, véase la figura 658, se aprecia también en este caso que el transitorio tiene una gran duración.
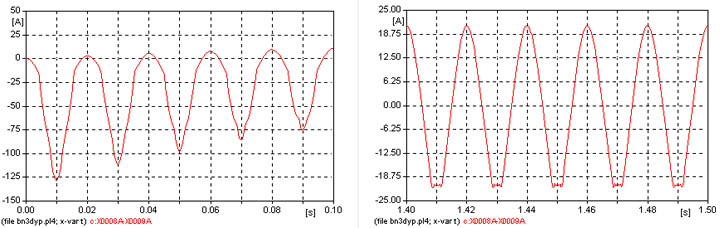
Inserción de transformadores en cascada
El figura 659 muestra dos transformadores en cascada que se insertan simultáneamente con el cierre del interruptor, la corriente de inserción del segundo transformador es corriente de carga del primero.
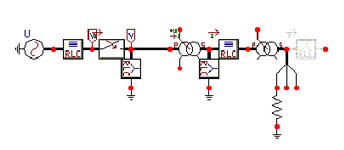
El ejemplo corresponde a transformadores de alimentación de horno eléctrico con tensión secundaria muy baja (500 V) y relativamente muy elevada tensión de alimentación, la solución constructiva se logro con dos transformadores en la misma cuba sin interruptor intermedio.
Es entonces de interés comparar la corriente de inserción de ambos transformadores en cascada, con la que se presentaría al conectar sólo el primero.
En la figura 660 obsérvese la corriente en el primario del primer transformador de la fase donde se presenta el pico.
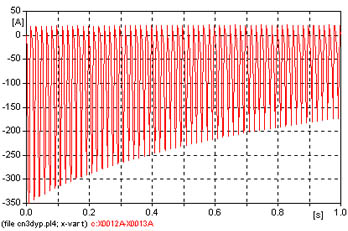
En la figura 661 obsérvense ambas corrientes que para hacerlas comparables directamente se representado en escalas adecuadas (en escalas de potencias - se multiplicaron por las tensiones).
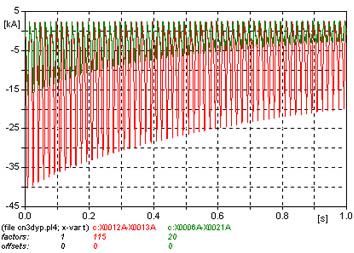
En la figura 662 obsérvense los primeros ciclos de la corriente de inserción.
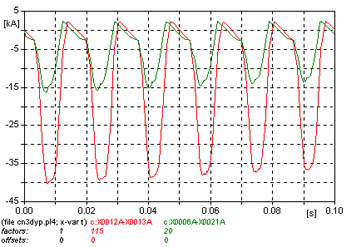
El figura 663 corresponde a la inserción de sólo el primer transformador, habiéndose desconectado el segundo.
La figura 664 muestra la corriente de inserción de sólo el transformador del lado de alta.
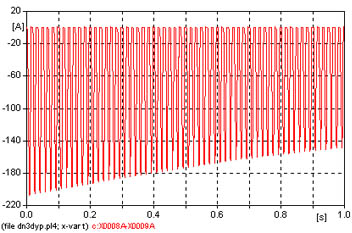
La corriente de inserción es menor, que la lograda para el caso de ambos transformadores en cascada.
Veamos ahora por último, que sucede al insertar el segundo transformador después de finalizado el transitorio de inserción del primero, en la figura 665 en los primeros instantes se observa la corriente de vacío y luego el efecto de la inserción.
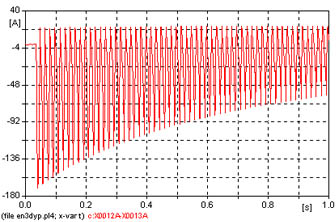
Obsérvense en la figura 666 ambas corrientes que para hacerlas comparables directamente se han representado en escalas adecuadas (en escalas de potencias - como antes se multiplicaron por las tensiones).
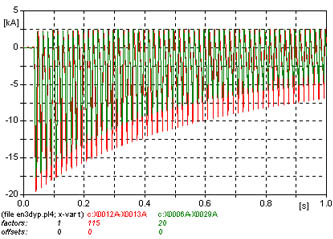
Obsérvense en la figura 667 los primeros ciclos de la corriente de inserción, y en la figura 668 los ciclos próximos a 1 segundo.
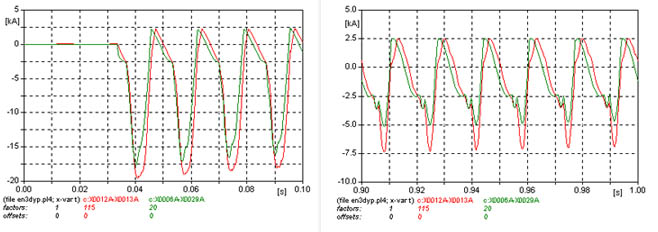
Comparación de los casos:
| Tabla VI | Corriente en 115 kV | I á 115 | p.u. | I á 20. | p.u. |
| Inserción de dos simultáneos | 346 | 39.8 | 1.746 | 14.5 | 0.636 |
| Inserción del primero | 198 | 22.8 | 1 | - | - |
| Inserción del segundo | 163 | 18.7 | 0.820 | 17.5 | 0.767 |
Se puede afirmar que cuando se insertan los dos transformadores en el primero es como si se presentara la suma de las corrientes de inserción (pico relativo 1.746 referido a 22.8), mientras que si se insertan uno a uno, el primero es como si sufriera dos inserciones, con picos máximos inferiores (1 y 0.820 tomados con la misma referencia).
Si se desea evaluar la corriente de inserción de ambos transformadores se observa que ésta es aproximadamente suma de los picos que se han presentado por separado (1 + 0.820 = 1.820 compárese con 1.746 correspondiente a la inserción de ambos).
Durante una energización (corriente de inserción) se presenta una carga dinámica similar a la que se tiene durante el cortocircuito de un transformador.
Los conductores del devanado están sometidos a una fuerza mecánica que es proporcional al cuadrado de la corriente, que se tiene en el caso más desfavorable (máxima asimetría).
Comparando el caso de inserción simultanea con las dos inserciones hechas sucesivamente, se observa que el primer transformador experimentara con la inserción simultanea un esfuerzo proporcional a 1.7462 = 3.048, mientras que al hacerse las inserciones en sucesión se tendrá primero un esfuerzo proporcional a 12 = 1 y cuando se inserta el segundo (una vez finalizado el transitorio de inserción del primero) a 0.8202 = 0.672, obsérvese que los esfuerzos son apreciablemente menores.
Conclusiones
Del estudio realizado se observa la ventaja de poder obtener por medio de los cálculos de dimensionamiento del transformador (TRADIM), los datos que ATP requiere, y no siempre disponibles a través de los protocolos de ensayo.
Con estos se puede preparar el modelo adecuado y realizar con el ATP el cálculo de las corrientes de vacío y de inserción teniendo en cuenta los distintos tipos de conexión, (pudiendo comparar estos resultados con los obtenidos mediante cálculos, más simples, independientes del tipo de conexión), el modelo puede incorporarse a configuraciones de red más complicadas donde influyen otros elementos.
Para distintos casos de conexión y para flujos vinculados o no vinculados, se observan las diferentes magnitudes y formas de la corriente magnetizante.
Sin tener en cuenta la magnetización residual del núcleo, para la inserción, se observa la influencia que tiene el tipo de conexión en la corriente de pico, el pasaje de la tensión por el valor máximo, la incidencia de que el transformador esté en vacío o con carga inductiva en la duración del transitorio, etcétera.
Con esta metodología, quien utiliza los transformadores podrá comprobar como se comportan en su instalación, además conocer parámetros que habitualmente (todavía) no suministra quien los construye, también brinda a quien tiene la responsabilidad de realizar el proyecto de las protecciones información que permite una mejor utilización y ajuste de las mismas.
Bibliografía
- G. REBORA "Il calcolo delle macchine elettriche" Librería Editrice Politecnica - MILANO.
- M. BORSANI "Calcolo e progetto dei trasformatori industriali" Editoriale DELFINO MILANO.
- General Electric authors "Transformer engineering" John Wiley & Sons.
- Rule Book Alternative Transient Program.
- Theory Book Electro-Magnetic Transients Program.
Copyright 2008 - 2012 INDUCOR INGENIERIA S.A. | Todos los derechos reservados | CCS| HTML