TECNICA DE LA ALTA TENSION
APENDICE 1
Problema 4.4
Nos proponemos estudiar el campo eléctrico que se presenta alrededor de una línea, una primera visión podemos tenerla observando el campo eléctrico de un conductor cilíndrico rectilíneo infinitamente largo que corre sobre el suelo a cierta altura figura 205 en un plano paralelo al zy perpendicular al conductor.
El programa POTESF nos permite hacer el modelo con un conductor de 2 cm de diámetro y a 6 metros de altura, por el método de las imágenes, representamos las equipotenciales desde 0 hasta 50 % en un área de 10 m x 10 m (en x de -5 a 5 y en y de 0 a 10 m).
Notamos que potenciales mayores de 50 % nos dan una densidad de líneas equipotenciales tal que sólo se ve una mancha. observamos entonces los potenciales de 50 % a 100 % en un área menor de 1 m x 1 m figura 206, y con paso de graficación menor figura 207 (entre -0.5 y 0.5 según x y 5.5 y 6.5 según y).
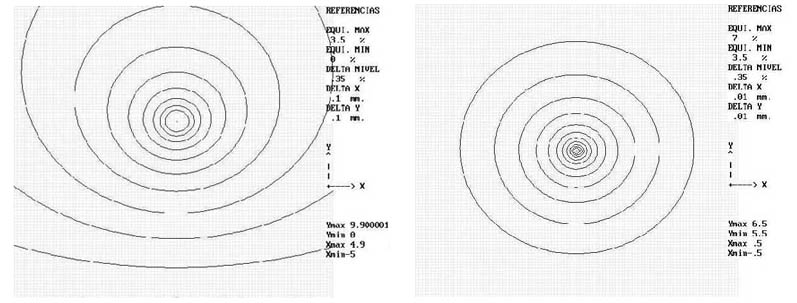
Nos interesa ahora acercarnos a la cadena de aisladores, representamos en POTRES la cadena, que está en una escala cualquiera, y contiene algunos aisladores que nos permite una cuadricula de 50 x 50, observamos de arriba hacia abajo la cruceta los aisladores y el conductor como se observa en la figura 205.
El corte de la cadena lo hacemos según el conductor, el área esta limitada por un contorno de líneas que serán normales a las equipotenciales, líneas de corriente o de campo. La cadena es de simetría cilíndrica sobre su eje, resolvemos el problema con simetría cilíndrica y con adecuado número de iteraciones resulta una gráfica satisfactoria figura 208 (y que no depende de continuar iterando).
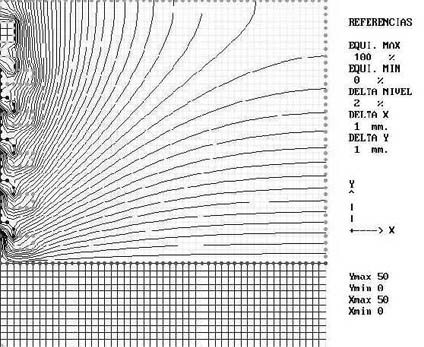
Interpretemos lo hecho, al hacer simetría cilíndrica el conductor se ha transformado en un disco plano normal al eje, los límites del área estudiada fuerzan las equipotenciales a ser normales al límite, el área de estudio es contenida, y los resultados no son válidos en partes del borde.
Aun así aceptando las hipótesis simplificativas tenemos una buena imagen del campo correspondiente al corte a lo largo del conductor.
Para completar el estudio hagamos ahora un corte de la cadena normal al conductor, también resolvemos el problema suponiendo simetría cilíndrica, el conductor resulta entonces una esfera en el extremo de la cadena figura 209.
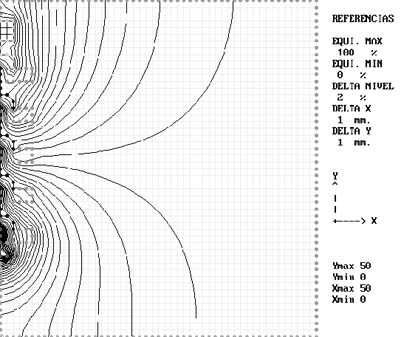
Miremos cualitativamente el conjunto de gráficas, al acercarnos a la cadena notamos que las líneas equipotenciales se acercan al conductor, mayor densidad de líneas significan mayor campo eléctrico, ¿cual es la razón de este aumento?
Recordemos que en la representación del cálculo el cable no está bien representado, de todos modos el último aislador de la cadena esta forzando una gran caída de potencial en la proximidad del conductor, que es la razón del aumento de campo en esta zona, que se debe controlar con un mejor diseño (o con anillos equipotenciales).
Una observación:
La cadena de aisladores nos ha obligado a forzar los potenciales intermedios de los aisladores, el programa POTRES no tiene capacidad de calcular potenciales flotantes (elementos intermedios metálicos de las cadenas).
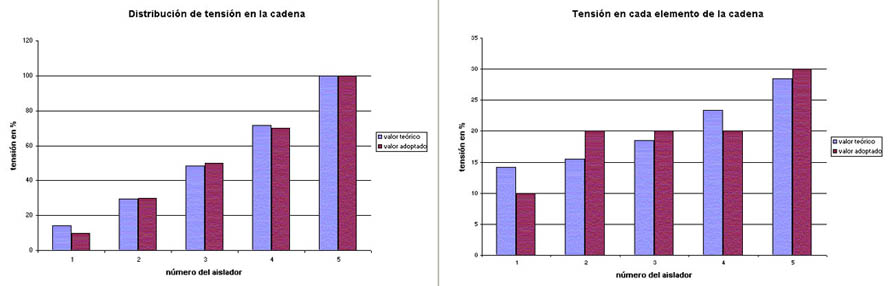
La bibliografía brinda ciertos valores de repartición del potencial en las cadenas, y estos se han redondeado a valores de 10 en 10 % que son los que el programa permite. Los valores de la bibliografía y los valores efectivamente asignados se muestran en la figura 210, la tensión en cada elemento de la cadena se muestra en la figura 211, observándose que la tensión sobre cada elemento es mayor cuanto más próximo está al conductor.

Copyright 2008 - 2012 INDUCOR INGENIERIA S.A. | Todos los derechos reservados | CCS | HTML



