TECNICA DE LA ALTA TENSION
CAPITULO 5 - AISLANTES SOLIDOS EN LA TECNICA DE LA ALTA TENSION
Intensidad de campo eléctrico y desplazamiento
Supongamos un capacitor conectado a una tensión alterna como se indica en la figura 101 Para una tensión de 50 Hz, el sentido de la tensión se invierte 100 veces por segundo, la carga Q del capacitor se desplaza 100 veces por segundo (a 60 Hz corresponden 120 veces) a través de la superficie de área A del dieléctrico. Se denomina a esta carga que fluye a través del dieléctrico como corriente de desplazamiento Q. Ella es igual a la carga del capacitor y está medida en Coulombs (C). La corriente de desplazamiento dividida por el área A, es el desplazamiento eléctrico D cuya unidad es C/m2.
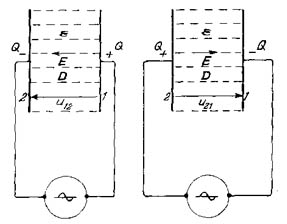
Tenemos:
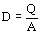
Entre el desplazamiento y la intensidad de campo eléctrico E, existe la relación:
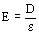
donde e es la constante dieléctrica del material aislante (dieléctrico). Está dada en kV/cm. D y E son vectores y tienen por lo tanto módulo, dirección y sentido.
Cálculo de la tensión a lo largo de las líneas de campo
Podemos distinguir dos casos:
Caso 1: Campo en el caso en que los vectores E y D son constantes. Entonces obtenemos para la tensión entre el punto 1 y el punto 2 a lo largo de una línea de campo la siguiente expresión:
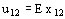
Si por ejemplo el camino de x12 está dado en mm, y E en kV/mm, se tiene u12 en kV.
Tratándose de un capacitor plano se tienen las siguientes relaciones:
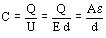
Siendo:
- Q carga eléctrica
- E campo eléctrico
- U tensión entre placas
- A área de las placas
- e constante dieléctrica
- d distancia entre placas
Caso 2: E y D son función de x. Entonces resulta:
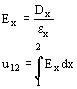
Con estas últimas expresiones podemos calcular la capacidad de un capacitor cilíndrico de dieléctrico homogéneo, despreciando la influencia de deformación del campo en los bordes del capacitor. Tal capacitor cilíndrico ideal es relativamente fácil de ser construido, haciendo un blindaje en los bordes y analizando solamente el campo eléctrico situado dentro del blindaje como se indica en la figura 102. De este modo, sólo la corriente i de los electrodos blindados es conducida por el dispositivo y las corrientes de los bordes son dirigidas directamente a tierra.
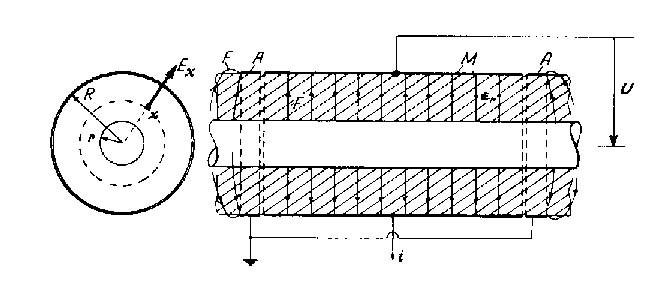
Llamando a la corriente de desplazamiento por unidad de superficie con Q, entonces el vector desplazamiento a través de una superficie cilíndrica de radio x dentro del dieléctrico, resulta:
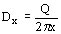
La intensidad de campo eléctrico, en la misma superficie, resulta:
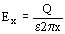
La tensión entre el electrodo interno de radio r y el cilindro conductor externo de radio R, a lo largo de las líneas de campo radiales, se puede calcular con la integral arriba indicada:
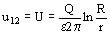
Relacionando carga y tensión resulta la capacidad y se tiene:
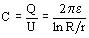
Finalmente haciendo otras sustituciones podemos expresar la intensidad de campo E en función del radio x:
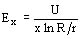
donde Ex está dado en kV/mm, si U está dado en kV y x en mm.
Dados el diámetro externo y la tensión del capacitor cilíndrico, la dependencia de la máxima intensidad de campo en función de la relación R/r tiene el aspecto que indica la figura 103. Cuando r es muy pequeño, entonces se tiene una gran intensidad de campo, debido a la gran curvatura. Si por otro lado, el valor de r es aproximado al valor R, el espesor del material aislante resulta pequeño, por lo cual se tiene igualmente una gran intensidad de campo.
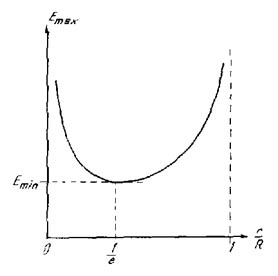
La intensidad de campo es mínima cuando el radio del cilindro interno r0 tiene el valor de 1/e = 1/2.718 del radio externo R, esta relación permite buscar condiciones de máximo aprovechamiento del aislante.
Capacitores planos con varias capas aislantes
En casos en que el dieléctrico de un capacitor plano se compone de dos (o más) capas de diferentes materiales aislantes la capacidad se calcula considerándose simplemente dos (o más) capacitores que están conectados en serie. Si los materiales tienen constantes dieléctricas e 1 y e 2:
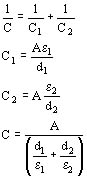
Interesa determinar el campo eléctrico en cada dieléctrico, lo que es una medida de la solicitación que se presenta sobre cada material.
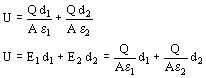
Capacitores cilíndricos con varias capas aislantes
En muchos casos, el dieléctrico de un capacitor cilíndrico se compone de dos o más capas de diferentes materiales aislantes. En este caso también la capacidad se calcula fácilmente, considerándose en este caso, simplemente dos o más capacitores que están conectados en serie. Para dos materiales con constantes dieléctricas e 1 y e 2 vale para una disposición como se indica en la figura 104:
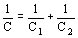
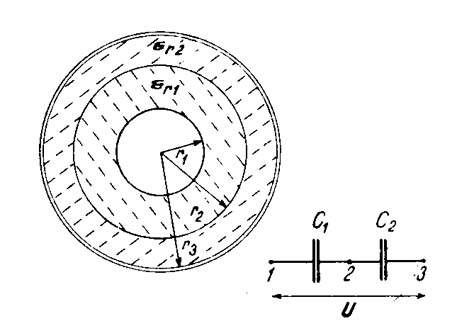
reemplazando las capacidades C1 y C2 y desarrollando se tiene para un capacitor cilíndrico de longitud l y de m capas aislantes:
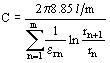
La tensión total aplicada al capacitor se distribuye en los distintos materiales como las constantes dieléctricas relativas e r1, e r2, e r3,... de tal modo que en una capa aislante, para la misma relación de radios, tenemos menor tensión cuanto mayor es la constante dieléctrica relativa de la capa.
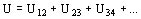
Esta expresión muestra que en un dieléctrico formado por varias capas, la intensidad de campo en una capa aislante es tanto mayor, cuanto menor es su constante dieléctrica.
El material con la menor constante dieléctrica posible es el aire (e r = 1). Por este motivo, capas de aire intercaladas en un material aislante sólido o líquido, asumen tensiones relativas mayores, o de otro modo, las intensidades de campo son mayores. Como el aire, a la presión normal poseen una rigidez dieléctrica baja con relación a otros buenos aislantes, es importante tener en cuenta el peligro de tener capas de aire en un aislante sólido o líquido.
Campo en cable de un solo conductor
Un cable de un conductor (en la jerga unipolar) es un capacitor cilíndrico con un dieléctrico homogéneo como capa aislante entre el conductor y la protección externa (y/o pantalla).
Según el tamaño del conductor (su diámetro) queda definido un espesor de aislación conveniente.
Las figuras siguientes muestran cables unipolares con aislación sólida (solución moderna) de distintas secciones y tensiones, pudiendo verse gran cantidad de detalles constructivos y alternativas posibles.
- Cable de 45 kV 630 mm2

- Cable de 110 kV 500 mm2

- Cable de 220 kV 500 mm2

- Cable de 400 kV 2000 mm2

Muchas aplicaciones en la electrotecnia de altas tensiones pueden, con buena aproximación, considerarse como capacitores cilíndricos y de esa manera ser fácilmente calculados. De este modo por ejemplo, los arrollamientos de los devanados de los transformadores y también de los devanados de las máquinas, dispuestos en el interior de núcleos magnéticos, pueden ser considerados perfectos capacitores cilíndricos si despreciamos los efectos de bordes.
Campo en cable tripolar
La capacidad por unidad de longitud de un cable tripolar se calcula con:
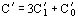
En la cual C´1 representa la capacidad unitaria entre conductores y C´0 la capacidad unitaria de cada conductor con relación a la pantalla a tierra del cable como muestra la figura 109
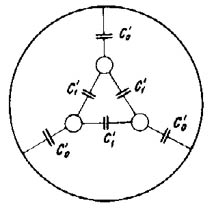
Se tiene una distribución de campo eléctrico menos favorable que en un cable de un solo conductor, o que un cable de tres conductores con tres pantallas independientes.
En un cable tripolar, la aislación envuelve cada uno de los conductores y además hay aislación de relleno que ocupa los vacíos. La aislación entre conductores se toca en los puntos P como se observa en la figura 110. La tensión entre estos puntos está representada en la figura por el triángulo vectorial P-P-P. El valor eficaz de tensión entre esos puntos resulta:
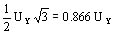
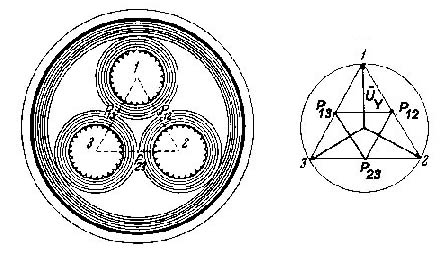
Como la rigidez dieléctrica de todos los materiales aislantes en sentido longitudinal es siempre menor que en el sentido transversal, se tiene en estos puntos una solicitación desfavorable, que puede dar origen a descargas que con el tiempo pueden destruir la aislación. Por este motivo, este tipo de cable no puede tener el dieléctrico tan solicitado como el cable de un solo conductor.
El cable aislado con papel impregnado constituye una de las primeras soluciones adoptadas y que ha perdurado para el transporte de energía con conductores enterrados.
Un cable para energía, aislado con papel impregnado, está constituido generalmente por uno o más conductores destinados a conducir la corriente eléctrica, revestidos por un material dieléctrico destinado a soportar la tensión eléctrica y por una vaina metálica que lo envuelve y lo separa del ambiente externo.
El cable puede ser del tipo a campo eléctrico radial y a campo eléctrico no radial. Al primer grupo pertenecen los cables en los cuales las líneas de fuerza del campo eléctrico están siempre dirigidas en forma radial, es decir en modo perpendicular al aislante, la figura 111 A, muestra un cable tripolar de este tipo.
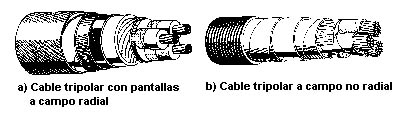
Al segundo grupo pertenecen en cambio aquellos cables en los cuales las líneas de fuerzas tienen también componentes tangenciales a las capas aislantes como arriba indicado, la figura 111 B, muestra este tipo de cable, y ya se ha comentado la más desfavorable condición de solicitación del dieléctrico.
Las pérdidas dieléctricas
Los capacitores con dieléctrico de material sólido o líquido, solicitados por tensiones alternas presentan un ángulo de pérdidas, que está originado por las pérdidas dieléctricas de los materiales. La tangente del ángulo de pérdidas se denomina factor de pérdidas.
La medida de la pérdida dieléctrica determina la calidad media de una aislación, ella no sirve para detectar pequeños defectos, como por ejemplo fallas del material, de una aislación que en su conjunto se presenta como buena. De todos modos la medida del factor de pérdidas es un óptimo control de la calidad del material, de la fabricación adecuada y principalmente para controlar el secado de una aislación.
Terminales de cables
Los cables aislados de media y alta tensión están formados por un cable conductor, una capa de semiconductor que hace cilíndrico el núcleo, una capa aislante de espesor uniforme más o menos importante según sea la sección, nuevamente una capa de semiconductor, de muy pequeño espesor, una pantalla electrostática, y por lo menos una capa de protección externa.
Cuando se termina el cable para conectar un aparato, si se piensa que la distancia en aire entre conductor y pantalla no puede ser el espesor del aislante, la idea intuitiva para incrementar esta distancia es agregar distancia en aire de la superficie cilíndrica del aislante, limpiando cierta longitud eliminando el semiconductor exterior.
El aislante puede quedar con forma cilíndrica, o se le puede dar forma cónica, la distancia entre conductor y pantalla puede alcanzar un valor suficiente, si se estudia el campo de un terminal así hecho se observa una gran concentración de campo en la proximidad de la pantalla, y el material aislante no soportará estas condiciones permanentemente.
Para mejorar la condición debe controlarse el potencial en esta zona, para lo cual se puede recubrir una parte del cilindro aislante con semiconductor de elevada resistividad, de esta manera se logra cierta distribución del potencial y se mejora la distribución de campo, la figura 112 A, muestra la distribución del campo eléctrico (las líneas equipotenciales) entre conductor y pantalla en el terminal.
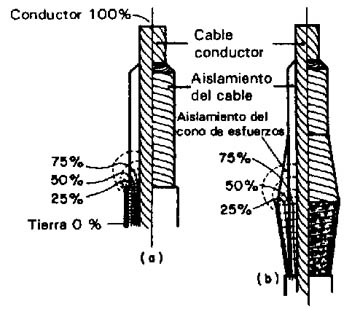
Otra forma de controlar el campo se logra agregando material aislante, dando al terminal que se construye sobre el cilindro una forma de dos troncos de cono, que partiendo del conductor crece primero, y luego decrece hasta el diámetro de la pantalla exterior, el cono que termina en la pantalla se recubre con semiconductor, y luego con una pantalla metálica, el otro en cambio queda de aislante limpio, ver figura 112 B.
Los troncos de cono se pueden realizar con cintas (vulcanizables) que se enrollan adecuadamente, con piezas sólidas prefabricadas, con material colado que fragua y se solidifica.
Los terminales para exterior se recubren con material aislante que soporta la intemperie, y que para controlar la contaminación tiene conos (polleras) que incrementan la línea de fuga.
En otros casos se introduce el terminal construido dentro de un aislador de porcelana hueco que cumple la función de protegerlo de la intemperie.
Para los cables aislados en papel impregnado de aceite (en particular fluido) el terminal se recubre con un aislador que contiene el aceite.
Los empalmes se construyen en forma parecida, se preparan los dos extremos, un manguito metálico une eléctricamente los conductores, el semiconductor se extiende sobre el manguito metálico dando formas suaves a la unión metálica, encima se coloca el material aislante, en espesor mayor al espesor del aislante en el cable natural, formando conos y un cuerpo cilíndrico.
Estos diseños inician de un cuidadoso análisis del campo eléctrico en el material aislante (dieléctrico), que debe evitar puntos que sean solicitados en exceso.
Aisladores para transformadores
De acuerdo con sus funciones pueden clasificarse en:
- Aisladores de línea
- Aisladores de neutro
- Aisladores de terciario
Los aisladores para transformadores y reactores tienen una extremidad destinada a funcionar en aire y la otra inmersa en el aceite aislante.
Los aisladores de línea son de papel impregnado en aceite, con repartición capacitiva, y están provistas de una derivación para ensayos.
Los aisladores de neutro pueden ser de papel impregnado con aceite, papel impregnado con resina, papel aglutinado con resina, moldeadas, de cerámica, etc., con o sin repartición capacitiva.
En los aisladores capacitivos se tienen cilindros conductores concéntricos, como se indica en la figura 113 (parte derecha), para formar superficies equipotenciales y mejorar la distribución de tensión.
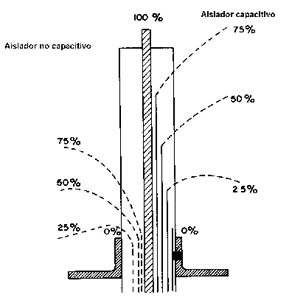
La derivación de ensayo se utiliza como capacitor de acoplamiento para realizar mediciones de descargas parciales.
Los aisladores tienen un tubo central, de cobre o aluminio, que puede ser conductor o permitir el paso de un conductor rígido o flexible. En los aisladores para bajas tensiones y altas corrientes, el conductor está constituido por un cilindro central macizo.
La porcelana, además de sus funciones aislantes, ofrece protección contra los agentes externos. La parte expuesta está formada por polleras, que proporcionan una distancia de fuga adecuada para las condiciones de polución existentes en el lugar de utilización.
En las especificaciones de aisladores para transformadores y reactores deben considerarse los siguientes aspectos:
- Tensión nominal del equipamiento
- Corriente nominal
- Nivel de aislamiento del equipamiento
- Sobretensiones
- Nivel de cortocircuito
- Características ambientales
Aisladores soportes
Cumplen la función de mantener separados de tierra las partes en tensión de las construcciones.
Los materiales que se utilizan son porcelana y materiales sintéticos.
La porcelana contrariamente a lo que se piensa es muy sólida y resiste en modo excelente las solicitaciones que se presentan.
Actualmente los aisladores de soporte han tomado forma de cilindro (aleteado para resistir la contaminación) como muestra la figura 114.
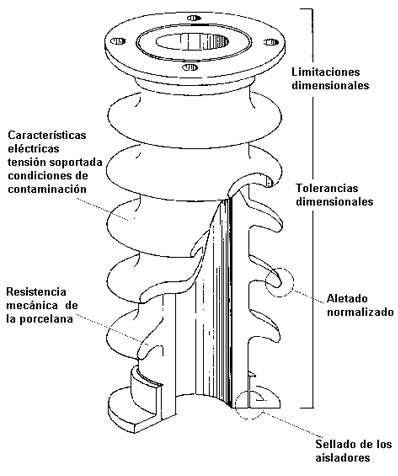
En los extremos se cementan piezas metálicas con el objeto de fijar el aislador al resto del equipo, o a la estructura.
Para la aplicación son de importancia sus características mecánicas, ya que los aisladores están exigidos por:
- Esfuerzos de cortocircuito
- Esfuerzos sísmicos
- Presión del viento
- Cargas de operación (cuando usados en equipos con movimientos)
Estas cargas presentan valores normales, valores excepcionales, y en algunos casos se deben considerar compuestas.
Aislación de arrollamientos de máquinas (descargas parciales, su efecto)
La aislación de las máquinas en la mayoría de las soluciones constructivas se realiza con capas de material aislante, que se tratan para que el dieléctrico quede lo más homogéneo posible, sin embargo el proceso constructivo puede hacer que queden capas de aire.
En el caso que se verifique una descarga parcial (ionización) en estas finas capas de aire, se tiene al mismo tiempo formación de ozono (O3). Como en las capas de aire existen siempre vestigios de agua (H2O) y naturalmente también nitrógeno (N2) y oxígeno (O2), se forma también en la descarga parcial en la capa de aire, ácido nítrico según la ecuación química:
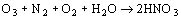
El ácido nítrico y el ozono destruyen con el tiempo la aislación y también el material conductor. Se alcanza de este modo la perforación eléctrica de todo el capacitor. Por este motivo los cables, durante la fabricación, deben ser completamente liberados del aire y la humedad, lo cual se logra con un proceso de secado en vacío en alta temperatura (alrededor de 100 ºC). Lo mismo es válido para otros materiales que deben trabajar con tensiones elevadas como por ejemplo los devanados de los transformadores de potencia y de medición.
Las estructuras aislantes en aire, como los arrollamientos de máquinas, no pueden lograrse totalmente libres de descargas. De algún modo la humedad del aire está siempre presente. De todos modos una buena aislación es posible utilizando adecuados materiales aislantes y procesos de fabricación.
Con esta técnica de aislación, difícilmente se construyen máquinas rotantes para tensiones superiores a 20 kV.
Recientemente se ha desarrollado un prototipo de máquina (generador) de mayor tensión, sus arrollamientos se construyen con cables de alta tensión.
Esta máquina experimental puede generar en una tensión de 45 kV, desarrollos futuros se espera alcanzaran mayores valores pudiéndose entonces alimentar directamente una red eléctrica en alta tensión sin la necesidad de interponer transformadores elevadores. El nuevo generador puede ser dimensionado para producir energía eléctrica en una gama de tensión de 20 a 400 kV con algunas ventajas respecto a los generadores convencionales.
Refracción de las líneas de campo
Dentro de un medio el campo es continuo, de un punto a otro vecino cambia solo infinitesimalmente, en la frontera, límite del medio, el cambio puede ser abrupto (tanto en magnitud como dirección).
Conviene observar el campo en la frontera a través de sus componentes normal y tangencial.
En la frontera entre medios e 1 y e 2 las componentes tangenciales de E son las mismas a ambos lados de la frontera figura 115:
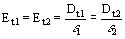
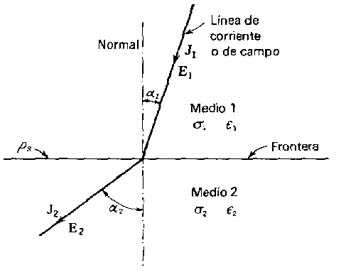
El campo eléctrico tangencial es continuo a lo largo de la frontera entre dos medios (las diferencias de potencial entre dos puntos en los dos medios son iguales).
El campo tangencial en la frontera conductor dieléctrico es nulo (efectivamente, el campo es normal al conductor).
Cuando un campo alcanza una superficie con una dirección cualquiera, se puede descomponer en una componente perpendicular a la frontera, que se comporta como un "amplificador" del campo en el dieléctrico con menor permitividad.
Veamos por ejemplo el caso de un aislador que tiene una frontera porcelana - aire, que obligará al campo perpendicular en aire a crecer entre 6 y 7 veces por ser el e r de la porcelana 6 a 7 veces mayor que el e r del aire.
Tan elevada concentración de campo, evidentemente, provocará descargas localizadas en el material que tiene menor e r.
La componente paralela a la superficie de la frontera, cuya intensidad es igual en ambos medios sólido y aire, actúa como "gatillo", uniendo los distintos puntos de descarga localizada que provocan las componentes transversales. De este modo sin alcanzar una elevada solicitación longitudinal se puede provocar la ruptura.
Se debe tener en cuenta que las aislaciones generalmente pueden tener un cierto grado de contaminación superficial. Esta situación contribuye a incrementar el efecto de "amplificación" transversal, deformando el campo eléctrico y concentrándolo en puntos específicos.
Este efecto se agudiza con la presencia de humedad, y la rigidez dieléctrica puede reducirse a 2 kV/cm o menos.
La forma aparentemente caprichosa de los aisladores sólidos en aire responde a distintas causas:
- Se deben equilibrar las solicitaciones transversales y longitudinales en la frontera, de modo que ninguna de ellas exagere su nivel.
- Se debe alcanzar la frontera con el mínimo gasto de material, previendo el efecto pernicioso de la contaminación.
- Se debe aumentar la zona protegida de los aisladores manteniendo algunos puntos libres de contaminación.
- Se debe permitir el rápido escurrimiento de agua, ya que en condiciones de lluvia se debe evitar la permanencia de contaminación húmeda en la frontera.
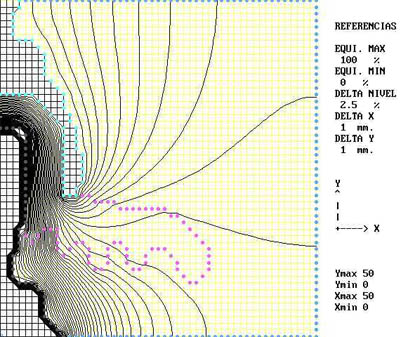
En la figura 116 se muestra un caso complejo e interesante de un aislador de campana, que muestra las correspondientes equipotenciales, observándose los puntos de quiebre donde se produce la refracción de las líneas de campo.
Determinación del campo eléctrico
La ecuación diferencial que se plantea para describir el potencial es de la forma
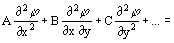
Según sea B2 - 4 A C se clasifica la ecuación, en elíptica (<0), parabólica (=0) o hiperbólica (>0).
Las ecuaciones elípticas corresponden a los problemas de campos eléctricos que finalmente se representan con ecuaciones de Poisson, o de Laplace.
Es difícil (si no imposible) resolver estos campos con métodos analíticos, por esta razón especialmente físicos e ingenieros han impulsado métodos numéricos, que fueron popularizados y difundidos por la posibilidad de usar las computadoras.
Los métodos numéricos pueden ser:
- De diferencias finitas, con una retícula rectangular
- De elementos finitos, aplicables a geometría cualesquiera
Las transformaciones de coordenadas permiten aplicar a geometrías complejas (curvas) los métodos de diferencias finitas (aplicables a geometrías rectangulares).
En los métodos de diferencias finitas, sobre el dominio se aplica una retícula regular, y se obtiene una ecuación de diferencias finitas aplicable a los puntos del dominio, con excepción de la frontera. Para la frontera se imponen condiciones (en general una condición mixta que fija la relación entre la solución y su derivada) y la ecuación de diferencias finitas aplicable en estos puntos es especial.
El caso general, con un retículo, presenta problemas en fronteras curvas, geometría no rectangular, para estos puntos se debe aceptar el error, o si se desea mejor solución es necesario actuar ajustando las diferencias, o aplicando al punto un método de elemento finito, o como se ha sugerido antes, aplicando una transformación de coordenadas que haga aplicable con la precisión deseada el retículo rectangular.
Si se plantea la ecuación de Laplace en diferencias finitas en un punto (0) del retículo (regular) caracterizado por una misma constante dieléctrica e en él y los puntos que lo rodean (1,2,3,4) se obtiene una relación:
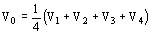
Si el valor de e es distinto en cada punto entonces se debe hacer un planteo similar pero considerando la constante dieléctrica, lográndose una relación más complicada.

Copyright 2008 - 2012 INDUCOR INGENIERIA S.A. | Todos los derechos reservados | CCS | HTML



